Открытие нуля – Как изобрели цифру, обозначающую «ничего»? История нуля | Обучение
Как изобрели цифру, обозначающую «ничего»? История нуля | Обучение
Сегодня это может казаться удивительным, но европейская математическая традиция долгое время не знала никакого нуля. И даже после того, как узнала, старалась подольше без него обходиться. И действительно — зачем нужно число, которое ничего не исчисляет? Бред какой-то… Да и первые европейские системы исчисления нуля не требовали, так как были непозиционными.
Одной непозиционной системой мы пользуемся до сих пор. Кому не знакома римская нумерация, которой мы обозначаем века, королей-тезок и разделы в книгах? Нуль в этой системе отсутствует. Число 20 записывается двумя десятками (ХХ=10+10), а 102 — сотней и двумя единицами (CII=100+1+1). Вроде бы всё просто, но вот беда — для каждого нового разряда надо выдумывать новый знак (I- 1, V-5, X-10, L-50, C-100, D-500, M-1000), иначе крупное число из одних единиц станет длинным и неразборчивым. Однако и с добавлением новых знаков числа часто выглядели громоздко. На постаменте знаменитого питерского Медного всадника написана дата открытия памятника — MDCCLXXXII. Сразу ли вы догадаетесь, что это 1782 год? Ну, а совершать подсчеты, оперируя такими числами, было еще труднее.
Впрочем, на практике никто палочками, птичками и крестиками не считал. Для этого использовали счётные доски — абаки. Абак в разных обличьях оказался весьма живучим изобретением. Только калькуляторам удалось вытеснить счёты, которыми в совершенстве владела еще моя бабушка-бухгалтер. Абаки и счёты были разделены на несколько позиционных рядов. Так, чтобы обозначить на счётах число двести семь, на первой проволоке (разряд единиц) отбрасывали в сторону семь костяшек, на третьей (ряд сотен) — две, а на второй (разряд десятков) ничего не отбрасывали, так как десятков в числе не было. Вот этот пробел, это пустое место и стало первым прообразом нуля. Говоря образно, нуль как число и цифра появился практически из ничего.
 Произошло это, конечно, не сразу. Одно дело — пустое место, другое дело — знак, и уж совсем третье — число. Первые шаги от пробела к знаку сделали вавилоняне. Их система счета была позиционной, как и наша, но если у нас каждый новый разряд в десять раз больше предыдущего, то у вавилонян — в шестьдесят. Суть позиционной системы заключалась в том, что каждый новый разряд записывался одними и теми же знаками, только располагали их левее предыдущего разряда. У вавилонян знаков было два: вертикальным клинышком обозначали единицу, а горизонтальным — десятку. Таким образом записывали числа до 59, а число 60 снова обозначали вертикальным клинышком. Как это выглядело, вы можете увидеть на рисунке внизу.
Произошло это, конечно, не сразу. Одно дело — пустое место, другое дело — знак, и уж совсем третье — число. Первые шаги от пробела к знаку сделали вавилоняне. Их система счета была позиционной, как и наша, но если у нас каждый новый разряд в десять раз больше предыдущего, то у вавилонян — в шестьдесят. Суть позиционной системы заключалась в том, что каждый новый разряд записывался одними и теми же знаками, только располагали их левее предыдущего разряда. У вавилонян знаков было два: вертикальным клинышком обозначали единицу, а горизонтальным — десятку. Таким образом записывали числа до 59, а число 60 снова обозначали вертикальным клинышком. Как это выглядело, вы можете увидеть на рисунке внизу.
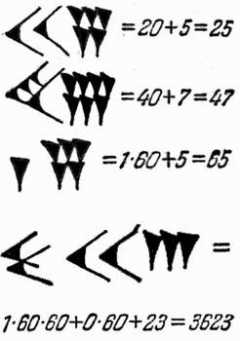
Родиной настоящего нуля по праву считают Индию, математики которой, судя по всему, совместили позиционный принцип вавилонян с десятичной системой китайцев. Гениальным итогом индийской математики стала запись любых чисел с помощью десяти цифр, которыми мы пользуемся поныне и которые не совсем справедливо называем арабскими (cами арабы, кстати, всегда называли их индийскими). Позже всех знаком наградили злосчастный нуль.
Само понятие нуля (индийцы называли его «сунья/шунья» — пустое) по-видимому возникло в середине V века. Первое же изображение нуля было обнаружено в числе 270, начертанном на стене г. Гвалиора (876 г.). Очень важно, что нуль здесь впервые стоит в конце числа и внешне напоминает знакомую нам дырку от бублика (разве что немного меньше других цифр). Форма нуля отобразилось и в нашей речи, ведь когда мы хотим оставить в числе только крупные разряды, заменив остальные нулями, то говорим «округлить».
Есть гипотеза, что сам знак нуля индийцы переняли у греков. Да-да, греческая непозиционная система годилась для небольших чисел, но для точных и громоздких астрономических расчетов Клавдию Птолемею приходилось пользоваться вавилонской системой — с ее помощью он записывал дроби. Вместо пропущенного разряда астроном ставил букву «О». Как и вавилоняне, в конце числа пропущенный разряд Птолемей не обозначал и числом не считал.
Заметьте, нуль имеет смысл лишь там, где мы говорим об отсутствии ЧЕГО-ЛИБО. В христианском богословии даже был прием доказательства бытия Божьего через отрицание. Он назывался апофатическим и заключался в том, что Бога определяли через то, чем он НЕ ЯВЛЯЕТСЯ. Так и нуль служит для исчисления ОТСУТСТВУЮЩЕГО в категориях, которые сами являются существующими. Разряд в числе — категория реальная и конкретная, но если он пуст, то мы употребляем для его количественной характеристики нуль.
 Возникновение нуля в десятичной позиционной системе сделало революцию в математике, облегчив как запись чисел, так и арифметические действия с ними. Арабы, вторгнувшиеся на территорию Индии в VII веке, не могли пройти мимо этого великого открытия. Они приняли индийскую систему и развили ее (множество математических терминов — алгебра, алгоритм — имеют арабское происхождение). Знаменитый математик Аль-Хорезми (IX в.) писал в своей книге «Индийское искусство счета»: «Если не остается ничего, то пишут маленький кружок, чтобы место не оставалось пустым. Этот кружок должен занять место, потому что в противном случае у нас будет меньше разрядов, и второй, например, мы можем счесть за первый».
Возникновение нуля в десятичной позиционной системе сделало революцию в математике, облегчив как запись чисел, так и арифметические действия с ними. Арабы, вторгнувшиеся на территорию Индии в VII веке, не могли пройти мимо этого великого открытия. Они приняли индийскую систему и развили ее (множество математических терминов — алгебра, алгоритм — имеют арабское происхождение). Знаменитый математик Аль-Хорезми (IX в.) писал в своей книге «Индийское искусство счета»: «Если не остается ничего, то пишут маленький кружок, чтобы место не оставалось пустым. Этот кружок должен занять место, потому что в противном случае у нас будет меньше разрядов, и второй, например, мы можем счесть за первый».
Кстати, долгое время слово «цифра» означала именно «ноль» и ничто другое (инд. «сунья», араб. «аль-сифр», лат. ciffra). От ciffra произошло множество названий, включая слова «шифр» и «зеро», хорошо известное любителям игры в рулетку. Позже термин «цифра» распространился на все знаки арабской нумерации. Слово же «ноль/нуль» вошло в обиход в XVI веке и произошло от греческого nullus — «никакой».
Через арабов индийская система счета пришла в Европу.
Одним из первых пропагандистов арабской системы в Европе был итальянский математик Леонардо Фибоначчи. В 1202 году он написал в своей «Книге абака»: «Девять индусских знаков суть следующие: 9, 8, 7, 6, 5, 4, 3, 2, 1. С помощью этих знаков и знака 0, который называется по-арабски zephirum, можно написать какое угодно число».
Реклама Фибоначчи не особо подействовала на европейскую профессуру, она предпочитала не связываться с подозрительными нулями и арабами и продолжала считать по старинке — с помощью античной системы или абака. Так, итальянский математик Джеронимо Кардан (1501−1576) умудрялся решать кубические и квадратные уравнения, не пользуясь нулем, что делало расчеты крайне сложными.
Зато арабскую систему сразу оценили далекие от высоких материй купцы и банкиры, она была незаменима для расчетов, и к XV веку торгаши пользовались ею вовсю. Окончательно десять арабских знаков утвердились в европейской науке лишь к началу XVIII века.
Причины столь стойкой неприязни к нулю заслуживают отдельного разговора, ибо коренятся в особенностях античного мировосприятия.
shkolazhizni.ru
История числа «ноль», его свойства :: SYL.ru
То, что математика является царицей наук, практически каждый из нас уяснил еще со школьных времен. Педагоги начальных классов с упоением рассказывали нам об этой науке, без которой сложно представить себе мироустройство. А тех упрямых, которые утверждали, что без математических знаний вполне можно прожить, учителя убеждали с помощью реальных примеров и интересных рассказов о цифрах. В дальнейшем мы начинали понимать, что умение оперировать цифрами может существенно облегчить взрослую жизнь, однако даже самые продвинутые ученики обычно упускали все, что связано с числом «ноль».
В школьном курсе математики ему не придавали особого значения, ведь главным было освоить простейшие правила совершения действий с ним. Однако, на самом деле, история числа «ноль» является одной из самых интересных загадок человечества. До сих пор раскрыть ее не могут ни историки, ни сами математики. Официальная версия предоставит вам сухой ответ на вопросы, «каким числом является ноль» и «когда он был изобретен». Но его настоящая история гораздо интереснее всего того, что вам могут поведать школьные и институтские учебники.

Немного о цифрах и числах
Вы когда-нибудь задумывались о том, как часто в течение дня вы сталкиваетесь с цифрами? Думаем, вы поразитесь, насколько плотно мы окружены ими в нашей повседневной жизни. Они являются буквально частью нас, поэтому сложно представить, что когда-то люди могли обходиться без математических знаний. Вы тоже так думаете? Тогда мы сможем вас удивить – человечество освоило счет еще на заре своего развития. Конечно, это еще нельзя было назвать математикой или системой счисления, похожей на современную, но все же из этих фактов становится понятным, что цифры, числа и счет сопровождают людей практически с момента осознания себя как индивидуума, имеющего некую собственность.
Однако история числа «ноль» началась еще не в те времена. Если считать, что цифрами люди в той или иной степени оперируют уже на протяжении тысячелетий, то лишь небольшой отрезок этого времени связан с числом, которое одновременно может обозначать пустоту и в разы увеличивать значение другого числа.
Ноль: понимание значения
Прежде чем рассказать, как появилось число «ноль», необходимо дать ему определение, которое раскрыло бы всю его внутреннюю парадоксальность. Некоторые математики считают данное число самым абстрактным и загадочным, приписывая ему по-настоящему мистические свойства.
Каждый ребенок в раннем детстве усваивает, что ноль – это пустота. Она имеет обозначение, но, на самом деле, не таит в себе абсолютно ничего. Но вот восточные ученые относились к ней абсолютно иначе. Практики Востока проводили параллель между пустотой, вечностью и бесконечностью. А к этим понятиям мудрецы подходили с большим уважением. Они видели в этом числе глубокий смысл и ставили его в числовом ряду на первое место.
Удивительно, но ноль, являющий собой пустоту, при расположении рядом с единицей, например, увеличивает ее в десять раз. Причем с каждым новым нулем число становится все больше. В этом и заключается парадокс числа, который не всегда под силу осознать людям. Ведь для того, чтобы появился ноль, человечеству пришлось перейти на новый уровень сознания и мышления. Не верите? Тогда давайте немного углубимся в историю.

Древние системы счисления
Как изобрели число «ноль», ученые могут только догадываться. Однако они четко представляют, какие системы счисления появились в истории человечества первыми. Специалисты утверждают, что счет как таковой возник благодаря необходимости понимать, каким запасом тех или иных вещей обладает человек. Изначально с этой целью использовались пальцы. То есть каждое число занимало свою определенную позицию в системе.
Такие модели стали называться позиционными и в дальнейшем они широко использовались разными народами. Пальцы быстро сменились ракушками, палочками, зарубками и камушками. Каждый предмет занимал свое место и подразумевал разряд или цифру. Однако нуля среди них не было, ведь для древних людей, пользующихся позиционной системой счисления, числа имели практическое значение. Они должны были обозначать реальное количество предметов или товаров, которые необходимо продать. Поэтому необходимости в числе, обозначающем пустоту попросту не было.
Римские цифры
В отличие от позиционной системы счисления римляне использовали в качестве обозначения чисел латинские буквы. Изначально для счета также брались камушки и после того, как один из них менял свою позицию, на его месте оставалось углубление. Если приглядеться, то оно очень напоминало сегодняшний нолик. Однако история числа «ноль» началась еще не в эти времена.
Римляне нашли очень удобным свой способ вести счет с помощью латинских букв, но и в этой системе древние ученые смогли обойтись без обозначения пустоты.
Греческие математики
В культуре эллинов числа имели очень большое значение. Математика серьезно влияла на развитие культуры и науки, поэтому было бы разумным, чтобы именно греки написали первую страницу истории возникновений понятий натурального числа и нуля. Однако это не так. Самим грекам ноль не был нужен. В первую очередь, они рассматривали числа под призмой геометрии, а эта наука отлично обходится без нулевого обозначения.
Примечательно, что ученые отлично понимали, что существует число, обозначающее пустоту. Однако в своих системах и сложных вычислениях они не оставляли для него места. При этом каждый из них представлял, чем число 55 отличается от 505, к примеру. Путаницы между ними не происходило, хотя свое обозначение ноль тогда еще не приобрел.

Первая символика числа «ноль»
В Вавилоне числа использовались повсеместно, однако принятая система была разработана еще шумерской цивилизацией и досталась вавилонянам в наследство. Она базировалась не на сегодняшней десятичной схеме вычислений, а на шестидесятеричной. Из-за этого расчеты древних ученых были крайне сложными и неудобные. Чтобы получить определенный результат, астрономам или математикам приходилось держать в голове массу вычислений, сделанных от единицы до шестидесяти.
Именно жители Вавилона первыми придумали присвоить нулю символ. На глиняных табличках число обозначалось изначально двумя палочками, а позже получило знак, напоминающий стрелу. При этом никаких математических действий с нулем не проводилось. Он не воспринимался как полноценная цифра, которая может повлиять на результаты арифметических расчетов.

Ноль в истории майя
Индейцы майя активно использовали в своих трудах двадцатеричную систему. Их понимание мира, религиозные верования и научные знания были очень глубоки, но во многом чужды и непонятны современным людям. Однако до сих пор ученых удивляет, насколько точными были вычисления, сделанные майя несколько тысячелетий назад.
Примечательно, что ноль они ставили в начало числового ряда и даже подарили ему название одного из дней. При этом число в их понимании не обозначало пустоту, скорее, его произношение было сходно со словом «начало». Подсознательно майя понимали, насколько глубоко понимание этого числа. Но все же они не использовали его в вычислениях. Удивительно, но ноль, играющий важное значение в календарях и других рукописных текстах, вовсе не воспринимался как самостоятельное число.
Индия – родина нуля
Большинство ученых считают, что история возникновения натурального числа и нуля обязана индийским ученым. Именно они подарили миру ту систему счислений, которой практически в неизменном виде мы пользуемся до сих пор. Считается, что математики из Индии сумели объединить в едином трактате все знания китайских ученых о десятичной системе счисления и вавилонскую позиционность. Мухаммед бен Муса в восьмом веке впервые в истории упомянул в своем трактате о нуле как о числе. В своей системе он записал его первым и доказал, что возможно совершать математические действия, используя это натуральное число.
В дальнейшем перевод трактата произвел настоящую сенсацию в Европе, хотя и попал туда только в двенадцатом веке. К этому периоду в Индии появилось еще несколько научных трудов, где более полно раскрывались значение и свойства нуля. В совместном трактате трех известных индийских математиков были даны примеры действий с числом «ноль». Появилось определение, что если из одного числа вычесть равное ему, то получится именно тот самый пресловутый ноль. Таким образом он сумел занять свое достойное место в числовом ряду и в дальнейшем начал активно использоваться при различных вычислениях.
В этот же период определился и символ загадочного числа. Изначально его обозначали точечкой, чуть позже она трансформировалась в аккуратный кружок. Индийцы определили, что с помощью десяти цифр можно записать практически любое число и сделали эти знания достоянием просвещённых людей всего мира.
Можно сказать, что таким образом в математике произошла революция.
Кто подарил нам слово «цифра»?
Быть может, вы не знаете, но именно нулю математика обязана появлением слова «цифра». Дело в том, что сами индийцы называли это число словом «сунья». В переводе оно обозначало «пустой» и как нельзя лучше характеризовало число «ноль». Однако арабы, которые позаимствовали у индийцев их систему счисления, по-своему перевели данное слово. На их языке оно стало звучать как «сыфр», что в дальнейшем трансформировалось в привычное нашему уху слово «цифра». С этого периода оно закрепилось и стало довольно широко использоваться.
Свойства числа «ноль»
Каждый школьник знает, что при сложении или вычитании нуля в результате получается исходное число. А вот если провести умножение, то произведение будет всегда равно нулю.
То, что делить на ноль нельзя, тоже известно со школьной скамьи. Однако многие математики рассматривают это действие отчасти как философский вопрос и строят вокруг него сложные теории.
Большое значение приобрело в математике появление отрицательных чисел. И у нуля на этой шкале особенное место. Это число является уникальным, так как оно не может быть ни положительным, ни отрицательным.

Применение числа в других областях знаний
С течением времени ноль приобретал все большее значение в науке. Постепенно он перешел и в другие сферы деятельности.
К примеру, сегодня всем известно, что долгота отсчитывается именно с нулевого меридиана. А на шкале Цельсия ноль разграничивает положительные и отрицательные температуры, являясь точкой замерзания воды.
Компьютерная кодировка также основана на применение нуля и единицы. На этом сочетании базируются все представления о программировании в мире. Без нуля данная система не смогла бы работать.

Интересные факты о ноле
Если вам кажется, что ноль – это скучно и неинтересно, то прочитайте нашу подборку интересных фактов об этом числе, и вы однозначно измените о нем свое мнение.
Немногим известно, что нулю был поставлен памятник в Венгрии. На сегодняшний день он является единственным числом, удостоившимся такой чести.
А вот жители Москвы имеют возможность загадывать желание на нулевом километре, обозначающим начало всех дорог в стране.
Единственная цифра, которую при всем желании невозможно записать римскими цифрами, – это ноль.
В истории человечества так и не появился нулевой год, его просто не существует как начальной точки отсчета.
Из всего написанного выше становится понятно, что ноль – это очень важная часть нашего современного мира. А изучение истории числа «ноль» может преподнести математикам еще немало сюрпризов, о которых сегодня пока еще рано говорить.
www.syl.ru
Как появилось число нуль?
На протяжении тысячелетий люди обходились без ноля: эта цифра была неизвестна ни египтянам, ни римлянам, ни грекам, ни древним евреям.
Первый в истории ноль изобрели вавилонские математики и астрономы. Еще около 300 г. до н. э. ученые Вавилона в своих расчетах вовсю жонглировали «воплощенным ничто» — нолем.
Ноль в представлении вавилонян выглядел совсем не так, как теперь. Он изображался в виде двух поставленных наискось стрел. В последующие века значение ноля стремительно возрастает. Ноль начинает занимать почетное место на различных числовых шкалах — например, на градусной. И ныне мы постоянно оперируем относительными показателями, то есть взятыми относительно некой условной — нулевой — отметки.
Независимо от вавилонян ноль изобрели племена майя, населявшие Центральную Америку. Они знали ноль и пользовались двадцатеричной системой счисления. Как и у вавилонян, ноль у майя был не числом, а лишь значком пробела и не участвовал в операциях сложения, вычитания, умножения и деления. Он лишь показывал, появившись, например, внутри числа «101», что в этом числе нет ни одной «двадцатки».
Лишь у индийцев впервые в истории человечества появляется ноль как математический символ, используемый в счетных операциях. Он появился, самое позднее, в 458 году нашей эры.
Поначалу индийцы пользовались словесной системой обозначения чисел. Ноль, например, назывался словами «пустое», «небо», «дыра»; двойка — словами «близнецы», «глаза», «ноздри», «губы», «крылья». Так, в текстах III — IV вв. н. э. число 1021 передавалось как «луна — дыра — крылья — луна».
Лишь в V веке великий математик Арьябхата отказался от этой громоздкой записи, использовав в качестве цифр буквы санскритского алфавита. А вскоре вместо букв ввели особые значки — цифры. Эта сокращенная форма записи позволила ярко выявить все преимущества десятичной системы счисления. Прежде чем «ноль» попал на Запад, он проделал долгий путь. В 711 году арабы вторглись в Испанию и завоевали почти всю ее территорию. В 712 году они захватили часть Индии и покорили Синд — земли в низовьях Инда. Там они познакомились с принятой индийцами системой счисления и переняли ее; с тех пор стали говорить (и говорят) об «арабских цифрах».
Персидский математик аль-Хорезми (787 — ок. 850) первым из арабов описал в своем трактате «Числа индийцев» эту новую систему счисления. Он посоветовал своим читателям ставить в расчетах пустой кружок на то место, где должно помещаться «ничто». Так на страницах арабских рукописей появился привычный нам ноль.
Купцы-мусульмане, посещая Китай, познакомили местных жителей с цифрой «ноль». К тому времени она носила уже новое название. Слово «шунья» («пустое») было переведено на арабский и стало звучать «сифр» и «ас-сифр». Нетрудно увидеть в этом названии прообраз таких слов, встречающихся в разных европейских языках, как «Ziffer», «Cipher», «Chiffre», «цифра».
Символика числа нуль.
Ноль имеет тот же символизм, что и круг. Изображенный в виде пустого круга, ноль указывает как на отсутствие смерти, так и на абсолютную жизнь, находящуюся внутри круга. Когда он изображается в виде эллипса, его стороны символизируют восхождение и нисхождение, разворачивание и свертывание. Перед единицей есть только пустота, или небытие, мысль, абсолютное таинство, непостижимый Абсолют.
Знак 0 — это исток всех чисел, и он недаром обозначается кругом, это предел бесконечно малых и бесконечно больших величин. Прозорливцы-математики давно перестали приписывать нолю значение пустоты. Ноль — сам себя замыкающий круг мира. Ноль — потенциал, еще не подвергшийся дифференциации, то есть непостижимый материал всех величин мира. Он обозначает полноту абсолютного Единства, а также олицетворяет Космическое Яйцо первичного андрогина, полноту. Так что, с одной стороны, ноль символизирует пустоту, ничто, смерть, несуществование, неявленное, отсутствие качества и количества, тайну. Но с другой стороны, ноль — это также и вечность, беспредельность, абсолютность действительности, всеобщность, потенция, порождающий промежуток времени.
Для Пифагора ноль — совершенная форма, монада, исток и простор для всего.
В Каббале ноль — безграничность, беспредельный свет, единое.
В исламе — это символ сущности Божества.
В буддизме ноль — пустота и безвещественность.
В даосизме ноль символизирует пустоту и небытие (Дао — прародитель единицы).
Свойства числа нуль.
В математике число нуль обладает только ему присущими свойствами.
- Любое число при сложении с нулем не меняется.
а+0=0+а=а
- Умножение любого числа на нуль дает нуль.
а*0 = 0 * а = 0
- Нуль не имеет знака (оно ни положительное, ни отрицательное).
- Так как при делении 0 на 2 получается целое число, то 0 является четным числом.
0 : 2 = 0
- 0 делиться на все числа, в результате получается нуль. Исключением является выражение 0:0, приводящее к неопределенности.
0 : а = 0
Памятники числу нуль.
Как мы уже убедились, число нуль удивительное во всех отношениях. Оно прекрасно. Было бы очень обидно, если бы число нуль не нашло отображение в памятниках искусства.
Точка, от которой отсчитывают расстояния в Венгрии, отмечена особо. В этом месте (оно находится в центре Будапешта) поставлен – ни много ни мало – памятник нулю. Ни одна другая цифра не удостоилась таких почестей!
В Дунайском биосферном заповеднике есть место, называемое «нулевым километром». Так называется место, где Дунай впадает в Черное море и откуда начинается отсчет расстояний на реке. Даже соответствующий монумент имеется. На острове Анкудинов, установлен знак нулевого километра. Отсюда ведется отсчет длины Дуная, пролегающего по землям десяти государств Европы. Интересно, что Дунай — единственная река в мире, которую измеряют не от истоков, а из дельты.
Также это число удостоилось памятника в городе Мюнхене.
Литература:
- http://xn--80aaiflkn.su/zagadki-pro-cifru-0/
- http://jtdigest.narod.ru/dig2_02/null.htm
- http://5klass.net/matematika-6-klass/Interesnye-fakty-o-chislakh/006-Osnovnye-svojstva-nulja.html
- https://infourok.ru/issledovatelskaya-rabota-po-teme-nul-eto-ne-polniy-nol-463926.html
- http://www.zaitseva-irina.ru/html/f1113023758.html
yun.moluch.ru
История нуля | Математика, которая мне нравится
Один из наиболее общих вопросов, который задают: кто открыл нуль? Ответить на этот вопрос в удовлетворительной форме невозможно. Если бы кто-то пришел к понятию “нуль”, а потом все увидели, какое это блестящее нововведение в математике, то на вопрос можно было бы дать удовлетворительный ответ, если даже было бы неизвестно, какой гений это придумал. Однако исторически возникновение этого понятия было совершенно иным. Неявно нуль появлялся, чтобы затем исчезнуть опять, как будто математики все еще искали его и не признавали его фундаментального значения даже тогда, когда нашли его.
Первое, что нужно сказать о нуле, это то, что имеется два варианта его использования, оба очень важные, но немного различные. Один путь – это указатель пустого разряда в нашей позиционной системе счисления. Так, в числе 2106 нуль служит для того, чтобы позиции 2 и 1 были верными. Очевидно, что 216 значит совершенно иное. Второй вариант использования нуля – это число, которое мы обозначаем 0. Имеются также разные аспекты применения нуля и внутри каждого из этих вариантов, а именно: понятие, обозначение и название. (Наше название “нуль” – zero – происходит в конечном счете от арабского “sifr”, которое также дало нам слово “цифра” — “cipher”).
Однако ни один из указанных выше вариантов не имеет истории, которую можно легко описать. Просто не получилось так, что кто-либо придумал идеи, а потом все начали их использовать. К тому же, нужно отметить, что нуль — далеко не интуитивное понятие. Математические проблемы возникли как практические, а не абстрактные задачи. Числа в ранние исторические эпохи имели более конкретное значение, чем то абстрактное понятие, которым они являются сегодня. Есть огромные мыслительные различия между пятью лошадьми и пятью вещами, и абстрактным понятием “пять”. Если люди в древности решали вопрос, сколько лошадей необходимо иметь фермеру, то ответом на него не могло быть ни 0, ни –23.
Можно подумать, что раз появилась позиционная система счисления, то нуль необходим как указатель на пустой разряд, тем не менее вавилоняне, у которых была позиционная система счисления, обходились без этого более 1000 лет. Кроме того, абсолютно не очевидно, что вавилоняне считали, что была какая-то проблема из-за существовавшей двусмысленности. Замечательно, что древние вавилонские работы по математике сохранились. Вавилоняне писали на табличках из обожженной глины клинописью. Символы выдавливались наклонным концом стила в мягких глиняных табличках и поэтому были клиновидными (отсюда и название — клинопись). Сохранились таблички, датируемые примерно 1700 годом до н.э., и мы можем прочитать оригинальные тексты. Конечно, их запись чисел отличается он современной (и основание системы счисления у них 60, а не современное — 10), но если перевести их числа в наши обозначения, то разницы между 2106 и 216 не будет (и понять, что они имели в виду, можно только по контексту). И только в 400 г. до н.э. вавилоняне начали использовать два символа клина в том месте, где мы бы поставили нуль, для обозначения того, что должно быть, 21”6 или 216.
Два клина были не единственным использовавшимся обозначением. Так, на табличке, найденной в Кише, древнем месопотамском городе, располагавшемся на востоке Вавилона, там, где сегодня находится юг центральной части Ирака, применялось другое обозначение. На табличке, относящейся примерно к 1700 году до н.э., для обозначения отсутствующего разряда в позиционной записи, используется три крючка. На других табличках, датируемых примерно тем же временем, используется для обозначения отсутствующего разряда только один крючок. Существует общая черта для различных обозначений пустой позиции. Они всегда используются между двумя цифрами и никогда на последнем месте. Так, хотя встречается 21”6, никогда не бывает 216”. Предполагается, что более ранний расчет на то, что контекста достаточно для понимания, еще применялся в этих случаях.
Если такая ссылка на контекст покажется глупой, то стоит отметить, что и сейчас мы его используем по отношению к числам. Если я поеду на автобусе в ближайший город и спрошу о цене на билет, то я знаю, что ответ “Три пятьдесят” подразумевает 3 фунта 50 пенсов. Хотя тот же ответ на вопрос о стоимости билета на самолет из Эдинбурга в Нью-Йорк подразумевает триста пятьдесят фунтов.
Отсюда видно, что раннее использование нуля для обозначения пустого места в действительности вовсе не использование нуля как числа, а просто применение некоторых знаков пунктуации, чтобы числа имели правильное значение.
Примерно тогда же, когда нуль появился в Вавилоне как указатель пустого разряда, свой вклад в математику вносят древние греки. Греки, однако, еще не приняли позиционную систему счисления. Стоит задуматься, какое это имеет значение. Как могли греки с их блестящими достижениями в математике оставить без внимания систему счисления, обладающую всеми преимуществами вавилонской позиционной системы? Мы дадим простой ответ на данный вопрос, хотя реальный ответ гораздо тоньше. Дело в том, что в основном достижения греков в математике были основаны на геометрии. И несмотря на то что в “Началах” Евклида есть книга по теории чисел, она также базируется на геометрии. Другими словами, греческие математики не нуждались в обозначении чисел, поскольку они оперировали числами как длинами отрезков. Числа, которые требовалось обозначать, использовали купцы, следовательно, разумного их обозначения не требовалось.
Были и исключения из описанного выше. Они касаются математиков, которые записывали астрономические данные. Здесь мы встречаем первый раз использование символа, который мы считаем сегодня обозначением нуля, для астрономов начали использовать символ О. Существует много предположений, почему применяли именно это обозначение. Некоторым историкам нравится объяснение, что это омикрон, который является первой буквой в греческом слове “ничто”, а именно в слове “ouden”. Нойгебауэр (Neugebauer) однако, отвергает это объяснение, поскольку греки уже применяли омикрон как число — оно обозначало 70 (греческая система счисления была основана на их алфавите). Другие предлагаемые объяснения стоят за “обол”, монету, почти не имевшую никакой ценности, и то, что О возникало, когда счетчики (ими были камешки или кости) использовались на доске с песком. Высказывается предположение, что когда счетчик убирали, чтобы оставить пустой столбец, на песке оставался отпечаток, похожий на О.
Птолемей в Альмагесте, который написан около 130 г. н.э., использует шестидесятиричную систему счисления и этот символ и на пустом месте, и в конце числа. И наконец, можно быть уверенными в том, что нуль начал обозначать пустой разряд. Это, однако, далеко от того, что произошло. Только немногие астрономы использовали такое обозначение, и оно выпадало из употребления несколько раз перед тем, как было принято окончательно. Идея нулевого места (конечно, не воспринимаемого как число Птолемеем, который все еще рассматривал его как своего рода знак препинания) в следующий раз появляется в индийской математике.
Теперь перенесемся в Индию, где, как справедливо было бы сказать, родилась система цифр и чисел, которая превратилась затем в достаточно сложную, ту, которую мы используем сегодня. Конечно, это не означает, что индийская система ничем не обязана более ранним, и различные историки математики думают, что использование нуля индийцы заимствовали у астрономов из Греции. Наряду с некоторыми историками, которым, казалось бы, совершенно необоснованно хочется приуменьшить вклад индийских математиков, есть и те, которые делают заявления об изобретениями индийцами нуля, заходящие слишком далеко. Так, Мукерджи утверждает: “…математическое понятие нуля… возникло также в спиритическом виде 17000 лет назад в Индии”.
Не вызывает сомнения, что использование нуля как числа пришло в индийскую математику около 650 г. н.э. Также индийцы использовали позиционную систему счисления, и нуль обозначал пустой разряд. В действительности есть свидетельства того, что нуль использовался для этого в Индии уже с 200 г. н.э., однако некоторые историки их отвергают, считая подделками. Давайте сначала рассмотрим последующее использование, поскольку оно продолжает рассуждения, приведенные ранее.
Около 500 г. н.э. Ариабхата (Aryabhata) разработал позиционную систему счисления, в которой еще не было нуля. Он использовал слово “ха” (“kha”) в разрядах, и оно впоследствии применялось как название нуля. Существуют свидетельства того, что в более ранних индийских рукописях для обозначения отсутствующего разряда применялась точка. Интересно, что в этих же документах иногда точка применялась для обозначения неизвестного, там, где мы могли бы написать x. Позже индийские математики давали название нулю в числах, записанных в позиционной системе счисления, хотя обозначения для него еще не было. Первая запись, касающаяся индийского ипользования нуля, которая всеми признается подлинной, датируется 876 г.
Это запись на каменной табличке, содержащей дату, соответствующую 876 г. Надпись относится к городу Гвалиор, в 400 км к югу от города Дели, где был разбит сад хаст, для выращивания достаточного количества цветов, чтобы 50 венков каждый день приносить в местный храм. И число 270, и число 50 написаны почти так же, как сейчас, только нули поменьше и слегка приподняты.
Теперь мы подходим к первому появлению нуля как числа. Давайте сразу заметим, что он ни в каком смысле не естественный кандидат в числа. С ранних времен числа — это слова, которые относятся к набору предметов. Разумеется, понятие числа становится все более абстрактным, и эта абстрактность позднее делает возможным рассмотрение нуля и отрицательных чисел, которые не возникают как свойства множества предметов. Конечно, проблема, которая возникает, когда кто-то пытается рассматривать нуль и отрицательные числа, состоит в том, как они взаимодействуют в арифметических операциях: сложении, вычитании, умножении и делении. В трех значительных книгах индийские математики Брахмагупта (Brahmagupta), Махавира (Mahavira) и Бхаскара (Bhaskara) попытались ответить на эти вопросы.
В XVII столетии Брахмагупта попытался дать правила включения в арифметику нуля и отрицательных чисел. Он объяснил, что если из данного числа вычесть его же, то получится нуль. Он дал следующие правила сложения, которые включают нуль:
сумма отрицательного числа и нуля есть число отрицательное, сумма положительного числа и нуля — число положительное, сумма двух нулей есть нуль.
Вычитание немного сложнее:
разность между нулем и отрицательным числом — число положительное, разность между нулем и положительным числом — число отрицательное, разность между отрицательным числом и нулем отрицательна, разность между положительным числом и нулем положительна, разность нуля и нуля — нуль.
Брахмагупта затем говорит, что если любое число умножить на нуль, будет нуль, однако с делением возникают трудности:
“Если положительное или отрицательное число разделить на нуль, то получится дробь, у которой в знаменателе нуль. Нуль, деленный на отрицательное или положительное число, есть нуль или выражение в виде дроби с нулем, стоящим в числителе и конечным числом в знаменателе. Нуль, деленный на нуль, есть нуль”.
В действительности Брахмагупта утверждает довольно мало, когда он предполагает, что , деленное на 0, есть . Очевидно, что здесь он затрудняется. Очевидно, он неправ, когда утверждает, что нуль, деленный на нуль, есть нуль. Однако это первая известная блестящая попытка расширить арифметику на отрицательные числа и нуль.
В 830 г., когда прошло около 200 лет после того, как Брахмагупта написал свой шедевр, Махавира пишет книгу Ganita Sara Samgraha, которая была задумана как обновление рукописи Брахмагупты. Он справедливо пишет, что
“…число, умноженное на нуль, есть нуль, и число не изменяется, если из него вычесть нуль”.
Однако его попытки улучшить утверждения Брахмагупты о делении на нуль, кажется, приводят его к неверному результату. Он пишет:
“Число остается неизменным, когда его делят на нуль”.
Так как это очевидно неправильно, мои слова “кажется, приводят его к ошибке” могут рассматриваться как заблуждение. Причина этой фразы та, что некоторые комментировавшие Махавиру пытались найти оправдания его неверному утверждению.
Бхаскара писал более чем на 500 лет позже Брахмагупты. И хотя прошло столько времени, у него все еще есть затруднения в том, чтобы объяснить деление на нуль. Он пишет:
“Количество, поделенное на нуль, становится дробью с нулевым знаменателем. Эта дробь называется бесконечное количество. В этом количестве, состоящем из того, что имеет делителем нуль, не происходит изменений, хотя к нему может быть многое добавлено и из него может быть многое вычтено, как никаких изменений не происходит в бесконечном и неизменном Боге, тогда как миры создаются и разрушаются, хотя многочисленные существа поглощаются или испускаются.”
Итак, Бхаскара пытается решить проблему записью . На первый взгляд, хотелось бы поверить, что Бхаскара пишет верно, но, конечно же, это не так. В случае, если бы это было правильно, произведение нуля на бесконечность было бы равно любому числу , так что все числа были бы равными. Индийские математики не могли прийти к точке зрения, что на нуль делить нельзя. Бхаскара, однако, верно установил другие свойства нуля, такие как .
Возможно, в этом месте мы должны заметить, что существовала другая цивилизация, развивавшая позиционные системы счисления с нулем. Это были люди майя, которые жили в Центральной Америке, на современной территории Гватемалы, Южной Мексики и Северного Белиза. Это была старая, но процветающая цивилизация, существовавшая с 250 до 900 гг. Мы знаем, что к 665 г. майя использовали позиционную систему счисления с основанием 20 и обозначением для нуля. Но применение нуля началось гораздо раньше этого времени и существовало до того, как они ввели позиционную систему счисления. Это замечательное достижение, к сожалению, на другие народы не повлияло.
Блестящие работы математиков из Индии распространились на запад, в арабские и исламские страны. Сначала они попали к Аль-Хорезми, который написал книгу Al’Khwarizmi об индийском искусстве вычислений, которая описывает индийскую позиционную систему счисления, основанную на цифрах от 1 до 9 и 0. Эта работа была первой в странах, где находится сейчас Ирак, в которой нуль использовался на месте отсутствующего разряда. В XII веке Ибн Эзра написал три трактата о числах, давшие возможность донести индийские символы и идеи десятичных дробей до внимания некоторых образованных людей в Европе. Книга чисел описывает десятичную систему для целых чисел, в которой разряды были расположены слева направо. В этой работе Ибн Эзра использует нуль, который он называет “galgal” (галгал, что значит колесо или круг). Немного позже в XII веке Аль-Самавал (al-Samawal) писал:
“Если мы вычтем из нуля положительное число, то останется точно такое же отрицательное, … если мы вычтем из нуля отрицательное число, то останется такое же положительное.”
Индийские идеи распространились на восток, в Китай, как и в мусульманские страны. В 1247 г. китайский математик Цзин Чиу-Шао написал Математический трактат в 9 главах, в котором использовал символ О для обозначения нуля. Немного позже, в 1303 г., Чжу Шицзе написал книгу Нефритовое зеркало из 4 элементов, в которой снова используется символ О для нуля.
Фибоначчи был одним из тех, кто сыграл важную роль в том, чтобы принести новые идеи о системах счисления в Европу:
“Важным связующим звеном между индийско-арабской системой счисления и европейскими математиками является Фибоначчи, итальянский математик.”
Примерно в 1200 г. в работе Книга абака (Liber Abaci) он описал девять индийских символов вместе со знаком нуль для европейцев, но этот труд долгое время широко не использовался. Важно, что Фибоначчи не был настолько смелым, чтобы трактовать нуль так же, как остальные цифры от 1 до 9, так как он говорит о “знаке” нуль, тогда как остальные знаки он называет цифрами. Хотя совершенно ясно, что появление индийских цифр в странах Европы имело большое значение, можно заметить, что в своем понимании нуля он не достиг ни глубины индийцев Брахмагупты, Махавиры и Бхаскары, ни арабских и исламских математиков, таких как аль-Самавал.
Можно было бы подумать, что развитие в целом систем счисления и в частности нуля должно быть с этого момента постоянным. Однако, это далеко не так. Кардано решил кубическое уравнение и уравнение четвертой степени без использования нуля. Его работа 1500 года была бы намного проще, если бы у него был нуль, но это не было частью его математики. К 1600 годам нуль начал широко применяться, но только после сильного сопротивления.
Конечно, проблемы, касающиеся нуля, до сих пор не устранены. Многие люди по всему миру отмечали наступление нового тысячелетия 1 января 2000 года. Конечно, они отмечали 1999 лет с того момента, как был создан календарь, ведь не было же нулевого года. Хотя можно было бы простить эту ошибку, немного удивляет, что большинство людей, кажется, неспособно понять, почему третье тысячелетие и XXI век начинаются 1 января 2001 года. Из-за нуля до сих пор возникают проблемы!
J. J. O’Connor and E. F. Robertson, A history of Zero. Перевод статьи http://www-history.mcs.st-andrews.ac.uk/history/HistTopics/Zero.html
hijos.ru
История числа ноль. Каким числом является 0?
Потребность в подсчёте стала очевидной для человека с самого начала формирования первобытного общества. Свои числовые системы, со специфическими цифровыми обозначениями, формировались во всех обособленных центрах цивилизации: в Египте и Древнем Вавилоне, в Китае и Индии, у южноамериканских индейцев и в античной Греции. Математика прошла путь от простейшего подсчета предметов до решения сложнейших теорем топологии. При этом история числа ноль насчитывает только мизерную часть этого срока.

Числа и цифры
От латинского nullis («никакой») произошло слово, обозначающее одно из важнейших математических понятий. Оно включает не только символ – цифру, помогающую вести счет, записывать математические операции. Это целая концепция. Отсутствие какого-либо количества, пустота, начало и бесконечность — философское отношение к этим понятиям было различным в разные эпохи, в разных системах миропонимания.
Позиционные системы счисления
В доисторические времена вести исчисление помогали пальцы рук и ног. Деление чисел на пятерки и десятки, происхождение десятичной системы счисления связано именно с этим. В дальнейшем для облегчения этих операций в ход шли зарубки на дереве и костях животных, засечки на камнях, камешки. ракушки и другие мелкие предметы. Каждый такой элемент обозначает конкретное число. Подобную природу имеют самые практичные числовые модели. Такие системы называются позиционными – значение цифр при записи чисел определяется их позицией или разрядом.
Примером противоположной по подходу и применяемой до сих пор системы является способ записи чисел, дошедший со времен Древнего Рима. В ней для обозначения единиц, десятков, сотен применяются буквы латинского алфавита.
Абак
Счётная доска, состоящая из углублений, соответствующих определенным разрядам, в которые укладываются камешки или бусины, знакома культурам разных народов и эпох. Известны и другие разновидности абака – веревки с узелками или шнуры с бусинами. Следующей ступению в развития такого приспособления стали счеты, применявшиеся до появления калькуляторов.
История числа ноль – это процесс возникновения математического понятия и начало применения символа, его обозначающего. И абак, и счёты являются в некотором смысле и средством визуализации числового ряда. Пустое место в соответствующем углублении или отсутствующая костяшка на счетах делала абстрактное понятие нуля наглядным. Символ, обозначающий его, впервые появился у математиков и астрономов Древнего Вавилона.

Вавилонский знак пустоты
В цивилизации, рожденной в междуречии Тигра и Евфрата, была принята числовая система, унаследованная от древних шумеров. Она была позиционной – значение цифр зависело от положения относительно других чисел. Разработанная за 4-5 тысяч лет до н. э., она была построена на числе 60. Математические расчеты, которыми пользовались древневавилонские инженеры и астрономы, выглядели поэтому достаточно громоздкими и неудобными. Чтобы успешно оперировать числами, необходимо было помнить наизусть или иметь перед глазами результаты умножения всех чисел от 1 до 60.
Цифра ноль, или знак, принятый вавилонянами для обозначения разряда, выглядели как два поставленных под углом клинышка или стрелы. Этот символ был составной частью числа и не участвовал в арифметических действиях – складывать или умножать на него было нельзя.

Заокеанский ноль
Независимо от математиков Месопотамии свой ноль ввели в обиход индейцы Центральной Америки — майя и инки. Общим для обеих систем счисления было то, что они не развивали идею нуля как числа.
Древнеамериканская цивилизация оставила миру множество достижений в интеллектуальной сфере. Сложные календарные системы майя и инков – результат многовекового опыта астрономических наблюдений и сложнейших математических расчетов. Но никогда в их уравнениях цифра ноль не присутствовала в качестве числа, влияющего на результат математических операций.

Античный взгляд
Главным наследием древнегреческих математиков были их достижения в геометрии и астрономии. Числа в их представлении — это отрезки, имеющие начало, конец и определенную длину. Ноль — это число, не имеющее в этом случае практической ценности. Отрезок с нулевой длиной в античной математике и философии не имел смысла.
Одним из главных постулатов учения Аристотеля является фраза Natura abhorret vacuum – «Природа не терпит пустоты». Бесконечность, ничто, несуществование – эти категории не вписывались в античное мироздание. Поэтому современный смысл вопроса «каким числом является 0» был недостижим для Архимеда, Пифагора или Евклида, хотя похожий на ноль символ встречается в таблицах великого астронома Птолемея. Букву «Омикрон» (первая буква в слове οὐδέν – «ничего») он проставлял в пустых клетках.
Родина ноля — Индия
Что же изобрели индийские математики? Махавира (850 г.), Брахмагупта (1114 г.), Ариабхата (476 г.) — авторы трактатов, в которых во многом оформилась современная система записи чисел и правила основных арифметических операций. Историки считают, что десятичность системы счисления была заимствована индийцами у китайцев, а позиционный характер её – у вавилонян. Есть мнение, что символ нуля был также заимствован индийцами из работ Птолемея.
Первым из математиков, сформулировавшим законченную числовую систему, которая остается до сих пор в неизменном виде и служит большей части человечества, был Хорезми Мухаммед бен Муса (787-850), живший в Багдаде. В его «Книге об индийском счете» подробно описаны девять арабских цифр и дан ответ на вопрос: «Является ли 0 числом?» Упоминание нуля в этой книге считается первым. Латинский перевод этого труда, стал широко известен в Европе в XII веке и положил начало распространению восточных математических знаний.
В отличие от европейцев, вечность у восточных философов вызывала благоговение. Поэтому ноль в уравнениях древнеиндийских ученых окончательно стал не только символом отсутствия единиц в соответствующем разряде, но и натуральным числом, влияющим на результат вычислений. Прибавление ноля, умножение на 0 – всё это обрело значение осмысленных математических операций.
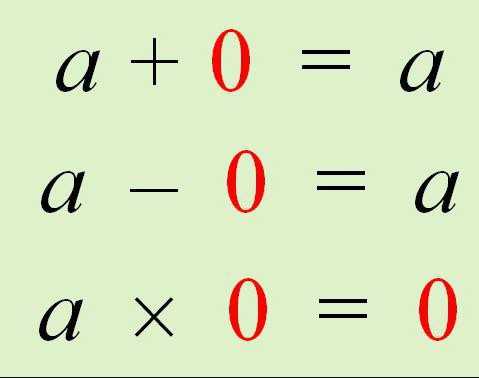
Само написание цифр от 1 до 0 обрело окончательный вид тоже благодаря древнеиндийским математическим трактатам, и те символы, что в Европе принято называть арабскими, сами арабы называют индийскими.
История числа «ноль» нашла отражение в этимологии основных математических терминов. Слово «цифра» имеет арабские корни и происходит от слова «аль-сифр», что означает «пустой, нуль». Английское «зеро» отдаленно напоминает «зефир» — ветер с востока, — именно с Востока в Европу пришла окончательно оформленная, рациональная и удобная числовая система.
Одним из главных европейских пропагандистов арабской цифровой системы стал знаменитый итальянский математик Леонардо Фибоначчи. Его труд «Книга абака» (1202) познакомил европейских ученых с символами и правилами, с помощью которых арабы записывают математические операции. Первыми удобство и рациональность восточной математической модели оценили те, кто привык к ежедневному обращению с числами, – банкиры и торговцы. Они быстро переняли от арабских купцов систему счисления и написание цифр. Но в научную практику Европы эти знания плотно вошли только через 4 века, сменив принятую европейскими математиками античную систему.
Важное значение ноль обрел с введением в научный обиход прямоугольной системы координат, предложенной в XVII веке Рене Декартом. Ноль, расположенный в центре, приобрел значение зримой и визуально понятной точки отсчета трех осей координат.
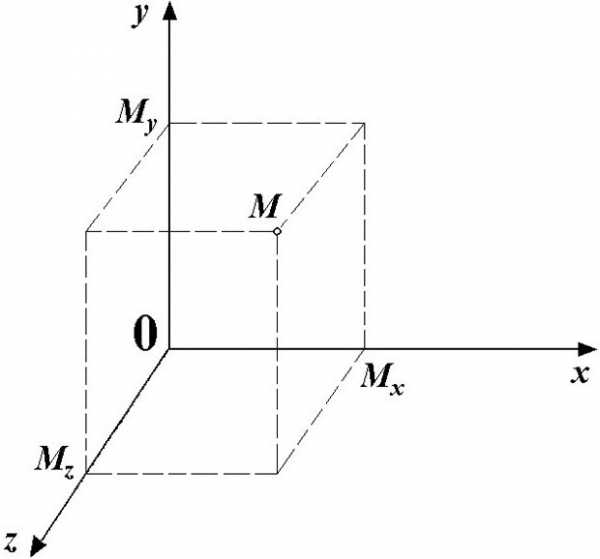
В России ноль вводился в практику стараниями Леонтия Магницкого, автора знаменитого учебника «Арифметика, сиречь наука числительная» (1703).
Свойства ноля
Ноль, который разграничивает положительные и отрицательные числа, обладает уникальными математическими свойствами. Это четное, не имеющее знака натуральное целое число. Сложение с нулем и вычитание нуля никак не влияет на число, а умножение на 0 даёт ноль. Деление на ноль считается не имеющей смысла операцией, которое в случае выполнения в компьютерной программе может нанести системе существенный вред.
Именно в попытке деления на 0 оказался смысл сбоя в компьютерной системе крейсера ВМФ США «Йорктаун», который произошел осенью 1997 года и привел к несанкционированному выключению двигательной установки. Некоректное отношение к числу, означающему «ничто», превратило мощный военный корабль в беспомощную неподвижную цель.
Значение этого числа существенно возрастало с развитием науки. Нуль возникает в областях не только чисто математических. Порог слышимости в акустике принимается за 0. Какое число стоит в начале шкалы многих измерительных приборов, известно и школьнику: 0 на шкале Цельсия – точка замерзания воды, начало отсчета долготы – нулевой меридиан и т. д.
Бинарное счисление, послужившее основой для создания современных вычислительных устройств, является позиционной системой счисления с основанием два. Это означает, что все данные, вводимые в компьютерные системы, кодируются сочетанием двух символов – единицы и нуля.

Роль компьютеров в современном мире становится определяющей для всех сторон жизни, а значит, история числа ноль, без которого их появление было бы невозможно, продолжается.
fb.ru
Как появился ноль | Современные педагогические технологии
Введение
Очень часто ученики интересуются историей возникновения чисел. Но мало кто задумывается, что такое ноль и кто его придумал. Ведь числа нужны были людям… А зачем нужен ноль? Почему одни люди говорят «ноль», а другие «нуль»? Кто из них говорит правильно? Мне стало это очень интересно…
Ноль (нуль, от лат. Nullus — никакой) — название первой (по порядку) цифры в стандартных системах исчисления. А также математический знак, выражающий отсутствие значения данного разряда в записи числа в позиционной системе счисления. Цифра ноль, поставленная справа от другой цифры, увеличивает числовое значение всех левее стоящих цифр на разряд. В голове не укладывается, но в средние века математики не знали такого понятия – и как-то обходились в своих сложнейших уравнениях без него.
Да, ноль – это ничто. Прибавьте ноль к любому числу – ничего не изменится. Вычтите ноль из любого числа – никаких перемен. И в то же время в царстве математики ноль обладает чудодейственной силой. Припишите позади цифры, начертанной вами, скромный, невзрачный нолик – воплощенную пустоту! Тут же значение цифры возрастет в десять раз. Попробуйте разделить на ноль, и на вас повеет бесконечностью. Наоборот, при умножении любого числа на ноль происходит крах: миллионы и миллиарды, соприкоснувшись с нолем, в ноль же и обращаются.
В данной работе узнаем кто, где и когда открыл ноль.
Итак, объект исследования: математика.
Предмет исследования: ноль
Цель исследования: Ответить на вопрос: Как появился ноль?
Задачи исследования:
· Изучить историю возникновения нуля у различных народов;
· Ответить на вопрос: Зачем нужен «Ноль» если это ничто?
· Ответить на вопрос: Как правильно говорить «ноль» или «нуль»?;
· Узнать, где кроме математики используется «нуль»;
· Сделать выводы и познакомить учащихся с результатами исследования.
Гипотеза: «Нуль — неотъемлемая часть жизни людей».
При работе над докладом мы пользовались следующими методами:
· поисковый метод с использованием научной и учебной литература, а также поиск необходимой информации в сети Интернет;
· наблюдение;
· анализ полученных в ходе исследования данных.
II. История возникновения чисел.
Давным-давно, многие тысячи лет назад, наши далекие предки жили небольшими племенами. Они бродили по полям и лесам, по долинам рек и ручьев, разыскивая себе пищу. Питались листьями, плодами и корнями — различных растений. Иногда ловили рыбу, собирали ракушки или охотились.
Одевались в шкуры убитых зверей. Жизнь первобытных людей мало чем отличалась от жизни животных. Да и сами люди отличались от животных только тем, что владели речью и умели пользоваться простейшими орудиями труда: палкой, камнем или камнем, привязанным к палке.
Первобытные люди, так же как и современные маленькие дети, не знали счета. Но теперь детей учат считать родители и учителя, старшие братья и сестры, товарищи. А первобытным людям не у кого было учиться. Их учителем была сама жизнь. Поэтому обучение шло медленно.
Наблюдая окружающую природу, от которой полностью зависела его жизнь, наш далекий предок из множества различных предметов сначала научился выделять отдельные предметы. Из стаи волков — вожака стаи, из стада оленей — одного оленя, из выводка плавающих уток — одну птицу, из колоса с зернами — одно зерно.
Поначалу они определяли это соотношение как «один» и «много». Частые наблюдения множеств, состоявших из пары предметов (глаза, уши, рога, крылья, руки), привели человека к представлению о числе. Наш далекий предок, рассказывая о том, что видел двух уток, сравнивал их с парой глаз. А если он видел их больше, то говорил: «Много». Лишь постепенно человек научился выделять три предмета, ну а затем четыре, пять, шесть и т. д. Учиться считать требовала жизнь. Люди научились записывать цифры. В разных странах и в разные времена это делалось по-разному. Многие тысячелетия люди могли обходиться без нуля благодаря непозиционным системам счисления. (Система счисления называется непозиционной, если в ней количественные значения символов, используемых при записи чисел, не зависят от места их положения в коде числа.)
Рассмотрим некоторые из них.
III. Непозиционные системы счисления
1. Ноль в Греции.
Греки пользовались несколькими числовыми системами. Лучшими были милетская и аттическая.
1) Милетская система счисления.
В милетской числовой системе единицы, десятки и сотни обозначались отдельными буквами греческого алфавита, например, альфа Αα (1), бета Ββ (2), гамма Γγ (3) и т.д. Поскольку в алфавите греков было всего 24 буквы, пришлось добавить еще три буквы, заимствовав их у семитских народов: буква «фау» стала означать 6, «копа» — 90, а «сампи» — 900. Тысячи обозначались теми же буквами, что и цифры от одного до девяти, только внизу перед ними ставили штрих. Число «десять тысяч» или по-гречески «мириада», обозначалось буквой М. Количество десятков тысяч помечали, надписывая над М соответствующие буквы. Именно этой системой записи пользовались такие знаменитые древние математики, как Архимед и Диофант. Чтобы написать, например, число 87, они обходились, как и мы, двумя символами, ставя рядом буквы «пи» (80) и «дзета» (7) : πζ
2) Аттическая система счисления.
знак | значение | название |
Ι | 1 | ἴος «иос» |
Π | 5 | πέντε «пенте» |
Δ | 10 | δέκα «дека» |
Η | 100 | ἑκατόν «гекатон» |
Χ | 1 000 | χίλιοι «хилиой» |
Μ | 10 000 | μύριοι «мюриой» |
В аттической системе записи использовались буквы «дельта» (10), «эта» (100), «хи» (1000), «ми» (10 000), «пи» (ее появление увеличивало число в пять раз; например, если рядом были написаны «пи» и «хи», эта запись означала 5000), а также штрихи, каждый из которых означал единицу.
Римский математик вынужден был использовать семь значков: LХХХVII, а египтянин – даже пятнадцать символов: восемь подков и семь вертикальных штрихов. Ясно, что оперировать такими числами на папирусе или пергаменте было очень неудобно.
2. Римская система счисления
Римляне использовали непозиционную систему счисления, которая сохранилась до наших дней, применявшаяся более двух с половиной тысяч лет назад.
В основе римской системы счисления лежат знаки I (один палец) для числа 1, V(раскрытая ладонь) для числа 5, Х (две сложенные ладони для числа 10, а также специальные знаки для обозначения чисел «I» (1), «V» (5), «X» (10), «L» (50), «C» (100), «D» (500) и «M» (1000).
Римскими числами пользовались очень долго. Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать).
Римская система счисления и сегодня используется для наименования знаменательных дат, томов, разделов и глав в книгах, для записи размеров одежды.
3. Ноль в Египте
Египтяне, греки и римляне предпочитали пользоваться счетной доской – абаком (подобные доски известны были и многим другим народам, например, китайцам и японцам).
Абаки имели несколько позиционных рядов – единицы, десятки, сотни. Если нужно было обозначить, например, 101 мешок зерна, в рядах сотен и единиц перебрасывалось в сторону по одной бусине, в то время как в ряду десятков между ними оставалось пустое место – фактически, наглядное воплощение нуля.
Превратившись в деревянные счеты, абак глубоко укоренился в культуре западных стран. С помощью этого несложного устройства подводили итоги финансисты Англии и немецкие бухгалтеры, китайские звездочёты и счетоводы России.
Примерно в третьем тысячелетии до нашей эры египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и так далее использовались специальные знаки. Вот они:
Все остальные числа составлялись из этих символов при помощи сложения.
Например: чтобы записать число 3252, рисовали три цветка лотоса (три тысячи), два свернутых пальмовых листа (две сотни), пять дуг (пять десятков) и два шеста (две единицы):
Величина числа не зависела от того как располагались его знаки: их можно было записывать сверху вниз, справа налево или вперемешку.
Используя приложение, я тоже попробовала записывать числа с помощью этих систем счисления. Вот что у меня получилось:
IV. Позиционные системы счисления.
Записывать числа, а тем более производить с ними арифметические действия было трудно из-за их громоздкой записи. Вот тут им и потребовалось, какое то универсальное число, которым и стал ноль.
1. Вавилонская нумерация.
Первый в истории ноль изобрели вавилонские математики и астрономы. Еще около 300 г. до н.э. ученые Вавилона в своих расчетах с легкостью жонглировали «воплощенным ничто» — нолем. Впрочем, слово «жонглировали» не вполне здесь уместно, если знать, как громоздка и неудобна была их математика.
В древнем Вавилоне примерно за 40 веков до нашего времени создалась позиционная нумерация, то есть такой способ записи чисел, при котором одна и та же цифра может обозначать разные числа, смотря по месту, занимаемому этой цифрой.
Наша теперешняя нумерация тоже поместная. В вавилонской поместной нумерации ту роль, которую у нас играет число 10, играет число 60, и потому эту нумерацию называют шестидесятиричной. Числа менее 60 обозначались с помощью двух знаков: для единицы, и для десятка. Они имели клинообразный вид, так как вавилоняне писали на глиняных табличках палочками треугольной формы.
Чем плохо было считать в такой системе счисления, сообразит каждый, вспомнив школьную таблицу умножения. Жители Вавилона, готовясь оперировать математическими значками, обязаны были помнить наизусть произведения всех чисел от «1 х 1» до «59 х 59» или хотя бы иметь под рукой обширную таблицу, где все эти произведения были перечислены.
Ноль в представлении вавилонян выглядел совсем не так, как теперь. Он изображался в виде двух поставленных наискось стрел. Таким образом, первоначально ноль был не цифрой, а лишь знаком пробела. Он не участвовал в математических операциях, а лишь помогал записать то или иное число и отличить их на письме. Так, тройка, за которой следовал пробел, превращалась в тридцать. Пробел был составной частью числа, но не числом. Складывать его с другими числами или умножать на него было невозможно.
Как же выглядели числа у вавилонян?
При записи чисел знаки для единицы, и для десятка повторялись нужное число раз, например:
Вавилонский способ обозначения чисел больше 60 очень похож на наш. В этом случае цифры записываются по разрядам, с небольшими пробелами между ними:
Так записывается число 302,
то есть 5х60+2:
А это 1х60х60 + 2х60 + 5 = 3725 :
При отсутствии разряда вставлялся значок , игравший роль нуля. Это запись числа 7203 (2х60х60 + 3):
2. Племена Майя.
Независимо от вавилонян ноль изобрели племена Майя, населявшие Центральную Америку. Племена Майя не знали, что такое колесо и упряжные животные, но познаниям в области математики им могли позавидовать многие. Они первые смогли определить по солнцу, что продолжительность года составляет 365,242 дня (современное измерение – 365,242198), а длина лунного цикла равна 29,5302 дням (современное измерение – 29,53059). Такие удивительно точные результаты были едва возможны без мощной системы записи числа. Посмотрим, как племена Майя делали это.
Жрецы и астрономы племени использовали систему счисления с основанием 20. У них ноль существовал, и, причём вполне реальный – в виде пустой раковины. Как и у вавилонян, ноль был не числом, а лишь значком пробела и не участвовал в операциях сложения, вычитания, умножения и деления. Он лишь показывал, появившись, например, внутри числа «101», что в этом числе нет ни одной «двадцатки». Первые 19 чисел выглядели так:
Многозначные числа большие 19, записывались вертикально, начиная с единиц высшего разряда сверху вниз. Например число 79 записывалось так:
Нетрудно заметить, что 79=3*20+19, т. е. цифру второго разряда определяли как произведение количества единиц на число 20.
Цифра третьего разряда определялась как число 360. Каждый следующий разряд считался следующим образом: цифра четвертого разряда рассчитывалась при помощи множителя 7200 (360 х 20), пятого – 144000 (7200 х 20) и т. д.
А число 13495=(1 х 7200+17 х 360+8 х 20+15) записывалось так:
За тысячу лет до индусов племена Майя уже использовали ноль в своей двадцатеричной системе исчисления. В календаре Майя месяц начинался не с первого, а с нулевого дня «Ахау». Ноль понимался не как «дырка от бублика», а как знак бесконечности, «начало» и «первопричина».
3. Ноль у Инков.
Что до культуры инков, то они могли бы снять собственную трилогию «Матрицы» — ведь их система счёта очень близка с двоичной системой исчисления, лежащей в основе работы современной техники. «Кипу» представляла собой верёвочные сплетения и узелки, в которых и содержалась вся информация. Учитывая, что шнурки разделялись на 24 цвета, из-за чего количество возможных комбинаций достигает 1536 – что в два раза больше, чем могли рассказать египетские иероглифы.
4. Индия и ноль.
Родиной ноля как полноценного числа считают Индию, а отцами – ученых-математиков Ариабхата и Брахмагупта. Ноль появился самое позднее в 458 году нашей эры.
Поначалу индийцы пользовались словесной системой обозначения чисел. Ноль, например, назывался словами «пустое», «небо», «дыра»; двойка – словами «близнецы», «глаза», «ноздри», «губы», «крылья». Так, в текстах III–IV вв. н.э. число 1021 передавалось как «луна – дыра – крылья – луна». Лишь в V веке великий математик Ариабхата отказался от этой громоздкой записи, использовав в качестве цифр буквы санскритского алфавита. Вскоре вместо букв ввели особые значки – цифры. Так, первым названием ноля было индийское слово «сунья» («пустое»). Первое его изображение выглядело как кружок, чуть меньший по размеру, чем прочие цифры – его нашли в записи числа 270, начертанном в 876 году на стене индийского города Гвалиора.
Эта сокращенная форма записи позволила ярко выявить все преимущества десятичной системы счисления. Опытный математик, жонглируя индийскими цифрами, мог перемножить два больших числа быстрее человека, переставлявшего костяшки на счетной доске.
Уже в VII веке индийские математики создают алгебру. Особенно больших успехов они добились в решении неопределенных уравнений, они использовали не только ноль, но и отрицательные числа.
V. Шествие «Нуля» по миру.
1. Ноль на западе.
Прежде чем «ноль» попал на Запад, он проделал долгий, окольный путь. В VII веке арабы вторглись на территорию Индии – и отсюда привнесли в свою науку новое понятие. Именно у арабов индийская система получила развитие и обросла новыми терминами – «алгебра», «алгоритм» и др. Здесь ноль назывался «аль-сифр», от которого происходит наше слово «цифра» (правда, применяемое ко всем 10 знакам, а не только нолю) – а от него произошло слова «шифр». Другое название – «zephirum», то есть «зефир», как ещё называют ветер (отсюда английское название ноля — «зеро»).
Через арабов позиционная система счета пришла в Европу – и хоть мы привыкли называть цифры «арабскими», они являются не иначе как индийскими, а сами арабы никогда не приписывали себе подобной заслуги.
Персидский математик аль-Хорезми (787 – ок. 850) первым из арабов описал в своем трактате «Числа индийцев» эту новую систему счисления. Он посоветовал своим читателям ставить в расчетах пустой кружок на то место, где должно помещаться «ничто». Так на страницах арабских рукописей появился привычный нам ноль.
Купцы-мусульмане, посещая Китай, познакомили местных жителей с цифрой «ноль». К тому времени она носила уже новое название. Слово «шунья» («пустое») было переведено на арабский и стало звучать «сифр» и «ас-сифр». Нетрудно увидеть в этом названии прообраз таких слов, встречающихся в разных европейских языках, как «Ziffer», «Cipher», «Chiffre», «цифра».
2. Ноль в Европе.
Европейцы знакомились с арабской ученостью, приезжая в Кордовский халифат – страну, в течение многих столетий занимавшую большую часть Пиренейского полуострова.
На рубеже 970-х годов в библиотеках Кордовы стал неизменно появляться некий приезжий в мусульманском одеянии. Это был переодетый французский монах Герберт из Орильяка, знавший греческий, арабский и еврейский языки и хотевший получить новые знания. Любознательный монах подвергся яростным нападкам со стороны священников, которые относились к языческим цифрам с неприязнью. Но остановить прогресс было уже нельзя.
Итальянский математик Леонардо Фибоначчи одним из первых заинтересовался индийской системой счёта, и не исключено, что именно его готовность к восприятию нового позволила ему сделать ряд важнейших открытий и закономерностей. Но его пропаганда столь удобного способа записи и счёта в своей «Книге Абака» не возымела особого действия на учёные средневековые лбы. И даже в 16 веке математики продолжали всячески избегать ноль, у пёрто придерживаясь античной системы и полагаясь на счётные доски. К примеру, итальянский математик Джеронимо Кардан (1501–1576) решал кубические и квадратные уравнения без ноля, совершая трудоёмкую и громоздкую работу безо всякой на то нужды.
Но, надо признать, эту простую и удобную систему сразу же оценили банкиры и купцы, которые считали вполне реальные деньги, а не извлекали воображаемые корни из воображаемых чисел в пыльной библиотеке. Уже в XV веке неакадемический люд вовсю считал с помощью индийских цифр, опережая учёные умы на столетия. Окончательно же десять знаков, включая ноль, утвердились в европейской науке лишь к началу 18 века.
3. Ноль на Руси
Здесь новая цифра появилась не так уж давно, и перекочевала, по всей видимости, уже из просвещённой Европы. В русском языке, ноль позаимствовали с немецкого языка ”NULL”. Привезли в Россию “NULL” ученые, во времена Петра I. До петровских времен вычислениями занимались с помощью римских цифр.
Леонтий Магницкий, который так же ввёл названия «миллион», «триллион», «биллион», «квадриллион», «множитель» и многие другие, на рубеже 17-18 столетий писал в своей «Арифметике» о ноле достаточно неуверенно. Так, математик называл его то «цифрой», то «ничем», то вообще «низачто». Математические рукописи XVII века ноль называли «оном» — из-за сходства с буквой «О».
VI. Ноль или нуль?
Итак, в России ноль появился сравнительно недавно. В словаре русских синонимов «ноль» определен следующим образом:
на голом месте плешь, ничто, шантрапа, десятая спица, не велика птица, последняя спица в колеснице, мелкая сошка, нуль без палочки, мелкота, зеро, маленький человек, ноль без палочки, никто, пятая спица в колеснице, шиш, ноль, нулевой цикл, козявка, ничтожность, пигмей, червяк, мелочь, червь, шишка на ровном месте, песчинка, пустое место, нолик, нулевка, ничтожество, пешка, тля, прыщ на ровном месте, мелюзга, мыльный пузырь, некомпетентный, нулик.
Сегодня «ноль» так прочно вошел в жизнь людей, что теперь представить ее без нуля просто невозможно. Но одни люди говорят «ноль», в другие «нуль». Как же правильно говорить?
Оказывается существуют две формы: ноль и нуль. В зависимости от того какие строятся предложения мы используем «ноль» или «нуль». Например, ноль целых, ноль внимания, в двенадцать ноль-ноль или нулевой меридиан, нулевой пробег, нулевой проводник.
VII. Заключение
«Ноль – это все, и все – это ноль», – говорят дзэн-буддисты, сращивая свою философию с математикой. Его появление было неприметно, его надобность вызывала сомнения, ведь за этим значком не скрывалось никакой реальной величины. Это пустяк, пустота, ничто! Мы не считаем графин в доме бесполезной емкостью, сосуд, который можно было бы выбросить. Согласитесь, на все есть свое время. Графин может какое то время оставаться пустым, затем, в каких-то случаях, мы захотим использовать его для наполнения жидкостью. И бесполезная вещь становится нам необходимой.
Между тем на этом пустом месте строится все здание современной математики. В цифре ноль таится намёк на неописуемое и невыразимое, в неё заключено беспредельное и бесконечное. В последующие века значение ноля стремительно возрастает. С появлением ноля произошёл настоящий переворот не только в банковском деле, но и в искусстве. В 1425 году итальянский архитектор Филиппо Брунеллески впервые в истории европейской живописи набросал рисунок, на котором все изображенные объекты сходились в одну центральную точку. Своим рисунком Брунеллески заложил основы центральной перспективы. Теперь – благодаря математической точности художника – плоское изображение производило впечатление трехмерного.
Ноль начинает занимать место на различных числовых шкалах. В географии он упорядочивает разные виды координат. Определяя долготу географического пункта, мы отсчитываем ее от «нулевого меридиана», проходящего через Гринвич. Все наше сознание насквозь математично – мы на каждом шагу подсчитываем плюсы и минусы, исчисляем дебет и кредит. Итоги, постоянно подводимые нами, немыслимы без понятия «ноль».
Наконец, без ноля не существовало бы современной компьютерной техники. Еще в первой половине ХIХ века немецкий инженер Конрад Цузе сконструировал первую электрическую вычислительную машину, которая оперировала цифрами «1» и «0». Ноль означал, что ток отсутствует, единица – что ток есть. Со временем на смену машине Z1 пришли ЭВМ. Но в основе их работы – все тот же принцип бинарного (двоичного) счисления.
А представить себе современную жизнь без компьютера уже так же трудно, как и то, что когда-то наши предки испытывали ужас перед цифрой «0».
pedtehno.ru
ГПД Открытие нуля.docx — ГПД Занятие 24. Открытие нуля
Лецких Л.А.
учитель начальных классов
МАОУ СОШ №21, г.Кунгур
ГПД Занятие 24. Открытие нуля
ОТКРЫТИЕ НУЛЯ
Р а с с к а з у ч и т е л я .
– Интересны были различные методы обозначения чисел, придуманные
египтянами и вавилонянами, греками и римлянами. Но у этих методов был один
недостаток: по мере увеличения чисел придумывали все новые и новые знаки.
Один из величайших древнегреческих математиков Архимед научился называть
громадные числа, но обозначать их он не умел. Не хватало ему самой малости.
Архимед, один из гениальнейших математиков в истории человечества, не
додумался до… нуля!
Знакомясь в первом классе с числом 0, мог ли ктонибудь себе представить,
что это одно из величайших изобретений в математике. Только после того как
люди научились обозначать пропущенные разряды в позиционной записи чисел,
они получили в руки могучее орудие познания природы. Без нуля не было бы
современной математики, не было бы и таких достижений человеческого разума,
как вычислительные машины и космические корабли.
Впервые нуль был придуман вавилонянами примерно две тысячи лет тому
назад. Но они применяли его лишь для обозначения пропущенных разрядов в
середине числа. Писать нули в конце записи числа они не догадались.
В Индии примерно полторы тысячи лет тому назад нуль был присоединен к
девяти цифрам, и появилась возможность обозначать этими десятью цифрами
любое число, как бы велико оно ни было. И самое главное, запись таких
гигантских чисел стала довольно короткой. Если бы живший 30 тысячелетий
тому назад древний человек имел представление о миллионе и захотел бы
изобразить это число с помощью зарубок на волчьих костях, ему пришлось бы
истребить 20 тысяч волков. А для записи миллиарда не хватило бы волков во
всех европейских лесах. Теперь же вся запись умещается в одной строке!
Приведем название некоторых больших чисел с указанием числа нулей после
единицы.
znanio.ru
