3Д фигуры: 3D фигурки — создание 3D фигурок под ключ, доставка по всей России!
3D фигурки — создание 3D фигурок под ключ, доставка по всей России!
3D фигурки
Создание 3D фигурок — логичное продолжение исторического ряда изобразительных искусств. Два века назад человек увековечивал себя на портретах, столетие — на фотографических снимках, полвека — на видео-записях и только в новом тысячелетии появилась возможность заказать фигурку на 3D принтере. Технология печати 3D фигурки на заказ — шанс получить точную уменьшенную копию близкого человека или домашнего питомца, важного объекта или любимого персонажа. Основой для изготовления сувенира могут являться:
● полученные в результате трехмерного сканирования данные;
● фотографии и видео-кадры;
● художественное изображение.
От вида носителя зависит точность передачи. Профессиональное сканирование непосредственно в нашем салоне на высокотехнологичном оборудовании. Работа с любым видом носителей позволяет добиться максимальной детализации конечно 3D модели. Итогом работы станет точная трехмерная копия с передачей цвета, пропорций и даже тонких черт лица.
Изготовление фигурок на 3D принтере — кропотливый и трудоемкий процесс, но такой презент вызывает восторг именно своей уникальностью и персонализированностью. В магазине готовых работ можно купить 3D фигурки востребованных тематик: звезды, лица масс-медиа и трендовые течения. Но какой будет сделанная по персональному заказу фигурка, решать только клиенту.
Оригинальное решение для каждого желающего как для подарка, так и для себя, вы можете заказать 3D фигурки любого предмета, даже вашей продукции, питомца или персонажа из известного мультфильма.
КАК СДЕЛАТЬ ЗАКАЗ
- Оставьте свою онлайн заявку на сайте, позвоните по номеру: +7 495 740 51 70 или отправьте свой запрос с приложением фотографий человека/объекта на почту [email protected]
- Мы производим расчеты и связываемся с Вами для уточнения всех деталей заказа в кратчайшие сроки.
- С учетом возможных дополнений согласовываем стоимость и сроки, заключаем договор.
- Приступаем к выполнению заказа.

- По готовности Вы можете забрать изделие посредством самовывоза или мы организовываем доставку любым удобным для Вас способом.
* * *
3d %d1%84%d0%b8%d0%b3%d1%83%d1%80 PNG пнг образ | Векторы и PSD-файлы
2022 год золотой рендеринг
3000*3000
Золотой 3d с новым годом 2022
1200*1200
Золотая круглая винтажная фоторамка 3d иллюстрация
2000*2000
значок instagram 3d сердце
1200*1200
Элемент вируса голубой цианы
1200*1200
концепция вакцины против коронавируса covid 19 бутылка и шприц 3d иллюстрация
3000*3000
как instagram 3d
3999*3999
новогодняя каллиграфия 3d рождественский дизайн элементы
2600*2600
3d телефон с прозрачным фоном
1200*1200
3d круглое сечение почвы земли с землей земли и зеленой травой
3000*3000
золотой 2022 3d прозрачный фон с золотым фейерверком
2500*2500
красные бактерии covid 19 изолированные на прозрачном фоне
1200*1200
Коричневая бумага для заметок 3d элемент
1200*1200
Коронавирус covid 19 бактерий 3d визуализации вируса
4000*4000
вирус короны 3d реалистичное изображение
1200*1200
Розовый двухслойный торт ко дню рождения 3d элемент
1200*1200
розовый 3d элемент вирус короны
1200*1200
3d как instagram
3999*3999
красное 3d сердце
1500*1500
3d золотой стиль
2600*2600
красивые яркие рождественские фонари 3d иллюстрации
1200*1200
Значок 3d как instagram
2000*2000
Значок 3d как instagram 02
2000*2000
день святого валентина 3d стерео любовь сердце
2000*2000
Текстура рамадан фонарь 3d луна
1200*1200
3d e золотой текстурированный шар
1200*1200
Мобильный телефон как 3d элемент
1200*1200
реалистичные фоторамка вектор 3d набор квадратных a3 a4 размеры дерева пустая рамка висит на прозрачном фоне с мягкой прозрачной тенью дизайн шаблона для макета
5000*5000
значок прямой трансляции 3d визуализация вид спереди
2000*2000
3d facebook live emoji в рамке для социальных сетей
1200*1200
3d день рождения стерео шар
1200*1200
против против 3d прозрачного фона
2500*2500
медицинская маска вид спереди 3d
1200*1200
рождественский подарок красный 3d упаковка
1200*1200
3d как instagram
1500*1500
Рождественская елка
1200*1200
3d новый год
1200*1200
3d как значок сердца
5000*5000
3d дизайн брызг воды
2400*2400
3d ленточная этикетка с тенью вектор дизайн веб элемент формы бокового текстового коробка баннер инфографики cdr
2000*2000
3d коробка подарков рождественская елка
1200*1200
День святого валентина 3d стерео любовь сердце
1200*1200
инфографики 3d лента этикетка с тенью вектор дизайн веб элемент форма заголовок текстовое поле баннер cdr
2500*2500
лучшие 3d нижняя треть заголовок изображений png панель имен тв социальные сети
2500*2500
пляжные путешествия 3d элементы
1200*1200
3d день рождения украшения разноцветные шары
1200*1200
синий корона вирус 3d элемент
1200*1200
2022 год золотой рендеринг
3000*3000
с днем рождения торт 3d элемент
1200*1200
летний сезон 3d брызги воды
2400*2400
Использование объектов в Paint 3D
Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).
Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).
С помощью Paint 3D можно создавать впечатляющие трехмерные объекты, но он также позволяет использовать большое количество готовых объектов в трехмерной библиотеке.
Примечание: Paint 3D доступен в Windows 10.
Поиск в библиотеке 3D-моделей
-
Запустите программу Paint 3D из своих приложений.
-
Выберите трехмерные фигуры на ленте, а затем откройте 3D-библиотеку.
-
Введите условие поиска в поле поиска и нажмите клавишу Ввод.

-
Выберите выбранную модель, чтобы добавить ее на холст.
Управление трехмерной моделью
С помощью трехмерных моделей можно перемещать их и добавлять кратные, чтобы создать собственную уникальную модель.
Позволяет делать Свинья с помощью Вингс!
-
При нажатии кнопки модель появится стрелка перемещения.
-
Стрелка вверх позволяет повернуть объект вдоль оси Z.
-
Стрелка вправо будет повернута вдоль оси X.
-
Стрелка вниз будет повернута вдоль оси Y.
-
Стрелка влево позволяет сдвинуть модель вперед и назад в пространстве.

-
Щелкните и перетащите модель, чтобы переместить ее по холсту.
-
Щелкните и перетащите небольшие белые квадраты на углы и стороны прямоугольника, окружающего объект, чтобы увеличить, уменьшить или растянуть объект.
Помещайтесь с ними, пока не получите хорошее представление о том, как перемещать модель и управлять ей.
-
-
Снова откройте 3D-библиотеку , найдите крыло, а затем найдите нужное, щелкнув его, чтобы добавить на холст.
-
Крыло появится на холсте. Перетащите модели и измените их размер, чтобы они выглядели так, как они будут объединяться.
-
Переместите модели до тех пор, пока крыло не будет правильно размещено, и кажется, что вы выйдете из свинья.

При нажатии кнопки выбрать все можно одновременно повернуть обе модели, чтобы убедиться в том, что они правильно работают со всеми углами.
-
Чтобы сделать две модели одной, щелкните выделить все и выберите пункт Группировать в правой части меню.
-
Дополнительные возможности: Добавление в трехмерную модель фона, эффектов и других возможностей
Способы
-
Вернитесь в 3D-библиотеку и выполните поиск нужного фона (например, небесно).
-
Щелкните объект заднего плана, чтобы изменить его размер и положение.

Перетащите углы фона на края холста.
Эффекты
-
Чтобы добавить эффект к проекту трехмерной заливки, нажмите кнопку эффекты.
-
Выберите нужный эффект в меню. Он будет быстро отфильтровать вашу закраску.
Щелкните солнце рядом с светло- кругом и поверните его, чтобы изменить положение освещения.
На других вкладках в верхней части Paint 3D (двумерные фигуры, трехмерные фигуры, наклейкии эффекты) вы можете добавить еще больше сведений в 3D-проект Paint.
Советы по Windows 10: как работать с основными инструментами Paint 3D
 Оно предоставляет вам простые в работе, но мощные графические инструменты. С их помощью вы можете комбинировать двумерные и трехмерные объекты, чтобы создавать творческие проекты любого уровня — для профессиональных целей или в качестве хобби. При этом вам не требуется никакой дизайнерский опыт: инструментами Paint 3D может пользоваться кто угодно. Доступный интерфейс позволяет легко перестраивать готовые трехмерные модели из встроенной библиотеки или создавать 3D-проекты с нуля.
Оно предоставляет вам простые в работе, но мощные графические инструменты. С их помощью вы можете комбинировать двумерные и трехмерные объекты, чтобы создавать творческие проекты любого уровня — для профессиональных целей или в качестве хобби. При этом вам не требуется никакой дизайнерский опыт: инструментами Paint 3D может пользоваться кто угодно. Доступный интерфейс позволяет легко перестраивать готовые трехмерные модели из встроенной библиотеки или создавать 3D-проекты с нуля.Основные инструменты Paint 3D
- Кисти. Уникальные перья и кисти, имитирующие настоящие материалы и не создающие беспорядка на столе, помогут вам проявить свои художественные способности. Попробуйте прозрачную акварель, которая красиво ложится на лист, или масляную краску, которая выглядит настолько реальной, что можно разглядеть каждый мазок. Эти художественные кисти можно использовать для рисования на двумерных и трехмерных моделях, применяя профессиональные эффекты, такие как полированный металл и матовый цвет, позволяющие персонализировать ваши проекты.

- Двумерные фигуры. Набор 2D-фигур и инструменты для рисования прямых и изогнутых линий позволяют быстро рисовать фигуры любой формы. Изгибы и углы можно настраивать с помощью узлов управления, появляющихся на фигуре при выделении. Нажав Make 3D («Превратить в 3D»), можно превратить фигуру в слой с дополнительными параметрами вращения.
Попробуйте сами! Перейдите по этой ссылке, чтобы просмотреть модель монтажной платы на сайте Remix3D. Загрузите эту модель в Paint 3D и используйте 2D-фигуры, чтобы добавить символы в схему. Затем добавьте волнистые линии с помощью инструмента рисования кривых. Советы по рисованию двумерных фигур смотрите в этом видео.
- Трехмерные фигуры. Начать работу в 3D можно разными способами. Например, можно создать новую модель на основе заготовок фигур. Или можно использовать инструмент 3D doodle, чтобы мгновенно превратить двумерные эскизы в трехмерные модели. Просто обведите объект на фотографии или нарисуйте что-нибудь самостоятельно — и вы мгновенно получите 3D-модель.
 «Остроконечный» 3D doodle позволяет создавать фигуры с острыми углами и идеально подходит, например, для рисования звезд. «Плавный» 3D doodle позволяет рисовать плавные линии, замечательно подходящие для изображения облаков.
«Остроконечный» 3D doodle позволяет создавать фигуры с острыми углами и идеально подходит, например, для рисования звезд. «Плавный» 3D doodle позволяет рисовать плавные линии, замечательно подходящие для изображения облаков.
Здесь вы найдете модель стула из библиотеки Remix3D. Загрузите ее в Paint 3D и попробуйте превратить в трехмерную модель, используя оба варианта 3D doodle. Посмотрите видео с советами по использованию инструмента 3D Doodle.
- Стикеры. Это уникальный и очень простой способ добавить к вашей модели подходящую текстуру. Попробуйте использовать этот инструмент и поэкспериментируйте с разными материалами, такими как дерево или мрамор. Или загрузите собственную фотографию и создайте из нее свой текстурный стикер. Стикер мгновенно «обертывает» трехмерные объекты, для его наложения не требуется никаких особых умений! После применения можно изменять прозрачность стикера.
- Текст. Добавляйте к моделям надписи, делая текст двумерным или трехмерным.
 Двумерный текст выравнивается по холсту и закрепляется на нем, тогда как трехмерный можно перемещать и вращать в разных направлениях.
Двумерный текст выравнивается по холсту и закрепляется на нем, тогда как трехмерный можно перемещать и вращать в разных направлениях. - Эффекты. Задавайте настроение проекта, изменяя окружение и освещение 3D-сцены с помощью эффектов. Например, создайте успокаивающую атмосферу с помощью эффекта Mist («Туман») или загадочную, применив эффект Night («Ночь»). Направление освещения можно менять, перемещая значок солнца по кругу.
- Canvas («Холст»). Цифровой холст имитирует полотно художника. На этой вкладке можно изменять размеры и управлять измерениями, например, отключать двумерный холст, чтобы он не мешал работать с трехмерной моделью.
- Magic Select («Волшебное выделение»). Этот простой в работе инструмент позволяет выделить часть изображения, которую вы хотите вырезать и удалить с фона. Выделение мгновенно перемещается на другой слой, а получившийся пробел устраняется интеллектуальными средствами автозаполнения.

- Библиотека 3D**. В нашем огромном каталоге можно найти тысячи бесплатных 3D-моделей для редактирования. Чтобы быстро начать работу, выберите любую модель из тематических коллекций или найдите подходящий объект с помощью поиска на панели инструментов. Одним касанием вы мгновенно импортируете 3D-модель в свой проект и сможете сразу же изменять и настраивать ее.
- Ползунок History («История»). Можно отменять и возвращать любые действия, без ограничений! Ползунок истории запоминает каждое изменение, позволяя возвращаться к предыдущим операциям. Можно даже записать видео о процессе редактирования, нажав на кнопку записи, а потом поделиться этим видео с друзьями.
- Режим трехмерного представления (3D view). В этом режиме можно рассматривать виртуальные объекты под любым углом. Можно увеличивать и уменьшать масштаб отображения, в том числе задавать точное значение масштабирования.
Здесь вы найдете сцену с акулой из библиотеки Remix3D. Загрузите эту модель в Paint 3D и используйте режим трехмерного представления, чтобы правильно разместить плавники. Затем используйте инструмент 3D doodle, чтобы добавить верхний плавник и установить его в нужное место.
Загрузите эту модель в Paint 3D и используйте режим трехмерного представления, чтобы правильно разместить плавники. Затем используйте инструмент 3D doodle, чтобы добавить верхний плавник и установить его в нужное место.
Посмотрите видео с советами по использованию режима трехмерного представления.
- Смешанная реальность. Трехмерную модель, созданную в Paint 3D, можно запустить в приложении Mixed Reality Viewer («Средство просмотра смешанной реальности»), чтобы визуализировать ее в контексте реального мира. Сделайте фотографию или запишите короткий ролик о том, как ваш трехмерный объект взаимодействует с вами в реальном мире, а затем отправьте друзьям.
Paint 3D поможет вам проявить творческие способности и воплотить свои идеи в жизнь. Запустите приложение Paint 3D и поэкспериментируйте с его функциями и инструментами. Если вы еще не знакомы с этим приложением, посмотрите видеоинструкции по работе в Paint 3D.
* Чтобы получить доступ к новейшим функциям Paint 3D, надо установить последнее обновление Windows 10: April 2018 Update. Подробнее о том, как получить обновление April 2018 Update, вы можете узнать здесь.
Подробнее о том, как получить обновление April 2018 Update, вы можете узнать здесь.
** Библиотека 3D доступна не во всех странах. Подробности здесь.
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings. DRAG_TEXT_HELP}}
DRAG_TEXT_HELP}}
{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings. CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}
CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}}
{{l10n_strings.CREATE_A_COLLECTION_ERROR}}ПК Альба Светодиодная 3Д фигура Новогодний подарок (с мишурой и гирляндой)
Объемные 3Д фигуры изготавливаются из алюминиевого каркаса, оформленного дюралатом и гирляндами. Это отличное украшение для торговых центров, скверов, площадей, территорий перед административными зданиями, садиками и школами. Такие композиции своей яркостью и необычностью привклекут взгляды прохожих и создадут праздничное настроение.
|
Высота |
0,6 м |
1,0 м |
1,2 м |
1,8 м |
2,3 м |
|
Ширина |
0,5 м |
0,75 м |
1,0 м |
1,5 м |
2,0 м |
|
Глубина |
0,5 м |
0,75 м |
1,0 м |
1,5 м |
2,0 м |
|
Мощность |
34 Вт |
56 Вт |
78Вт |
100 Вт |
186 Вт |
|
Цвет |
на выбор |
||||
|
Светодинамика |
фиксинг |
||||
|
Сиепень защиты |
IP 65 |
||||
|
Материал каркаса |
алюминий |
||||
Компания Альба не только продает светодиодные светильники, мы всегда готовы предложить комплексный подход к решению вопроса освещения. Именно поэтому, мы выполняем все работы: от составления проекта освещенности, на основании которого мы подбираем требуемые светильники и предлагаем способ их расстановки, до монтажа под ключ. Помимо установки светильников у нас есть опыт по монтажу опор, электрощитов, вплоть до проведения проводки внутри зданий.
Именно поэтому, мы выполняем все работы: от составления проекта освещенности, на основании которого мы подбираем требуемые светильники и предлагаем способ их расстановки, до монтажа под ключ. Помимо установки светильников у нас есть опыт по монтажу опор, электрощитов, вплоть до проведения проводки внутри зданий.
2D и 3D формы | 10 самых ценных различий для изучения
Различия между 2D и 3D формами
Объекты, которые нарисованы в двух измерениях, а именно X и Y, называются 2D-фигурами. При рисовании фигур, когда третье измерение или направление входит именно в направление Z, а форма, которая проецируется в направлении Z, называется трехмерными фигурами. В этой теме мы будем изучать 2D и 3D Shapes.
Эти фигуры нарисованы на одной плоскости независимо от направления, которое показывает различный внешний вид. Использование обеих этих форм является особенным и оказывается уникальным в той же области. Большинству людей, которые хотят изучать трехмерную форму, приходится проходить через 2D-фигуру, а затем они должны идти дальше. 2D является основой 3D, так как учащийся должен накапливать все 2D трюки, иначе ему становится трудно рисовать 3D фигуры.
2D является основой 3D, так как учащийся должен накапливать все 2D трюки, иначе ему становится трудно рисовать 3D фигуры.
Формы не имеют значения, но их плоскости определяют их размерность. Если мы проверим разницу между любой 2D-структурой и 3D-структурой, мы можем заметить разницу между 2D-и 3D-формами. Предположим, мы хотим узнать разницу между квадратом и кубом. Квадрат имеет 4 ребра и 1 грань, и если рассматривается куб, то он имеет 6 граней и 12 ребер. Это был бы правильный пример, чтобы объяснить разницу.
Обычно 2D-формы начинаются с того времени, когда мы были маленькими, когда мы рисовали небольшие эскизы в книгах для рисования и когда мы стареем, мы придерживаемся 3D. В графическом дизайне мы видим, что во время обучения мы должны накапливать все 2D-фигуры, такие как рисование круга, шестиугольника и т. Д. Мы используем это, чтобы начать рисовать цветок или любое другое маленькое существо.
Сравнение лицом к лицу между 2D и 3D формами (Инфографика)
Ниже приведены 10 основных отличий между 2D и 3D-фигурами:
Ключевые различия между 2D и 3D формами
Ниже приведены списки точек, описывающие ключевые различия между 2D и 3D формами:
- Основное ключевое различие между 2D и 3D-фигурами — это ось, которая находится под углом 90 градусов к двум другим осям.

- Фигуры, которые не показывают глубину или ширину объекта или структуры, являются 2D-фигурами, вместо этого в 3D мы можем видеть глубину или высоту.
- На технических чертежах 2D-образные чертежи трудно читать людям, не являющимся инженерами, вместо этого 3D-фигурные чертежи могут быть прочитаны многими людьми.
- Количество поверхностей и ребер больше в трехмерной форме по сравнению с двумерными фигурами.
- Когда мы хотим объяснить любой продукт с помощью 2D-форм, нам нужно нарисовать количество видов, таких как вид спереди, вид сверху, вид сбоку и вид снизу. Иногда нам нужно нарисовать больше видов в зависимости от продукта, но в 3D-виде мы можем очистить объективный вид клиента в одном виде.
- Размерно, если мы рассмотрим, то гораздо проще объяснить подробные размеры каждого отдельного края детали в двухмерных формах или чертежах. В 3 измерениях очищается только внешнее измерение, трудно показать все детали.
- По сути, когда мы рисуем вид в разрезе или детальный вид любой детали, небольшие объекты и скрытые объекты выделяются с помощью 2D-фигур.
 В трехмерных формах эта детализация невозможна.
В трехмерных формах эта детализация невозможна. - Тень любого объекта, нарисованного на бумаге для рисования, невозможно отобразить, когда мы рисуем в 2D-чертеже. Поскольку это шоу отражает другую ось или третью ось, а именно Z. Чтобы показать тень, нам нужно всегда рисовать в 3D.
- 2D-формы показывают основной эффект, такой как необработанные формы, доступные квадраты, пятиугольник, шестиугольник и т. Д., Который помогает рисовать любые сложные формы в программном обеспечении при рисовании любой 2D-формы. Вместо этого в 3D мы можем использовать эти квадраты в пятиугольнике, но не можем накапливать все вместе.
Сравнительная таблица 2D и 3D фигур
Ниже приведено лучшее сравнение двухмерных и трехмерных фигур.
| SR. Нет . | 2D Shape | 3D Shape |
| 1. | Он имеет 2 измерения, а именно X и Y. | Он имеет 3 измерения, а именно X, Y и Z. |
| 2. | Квадрат, круг и треугольник нарисованы с использованием 2D-фигур. | Куб, сфера и призма нарисованы с использованием трехмерных фигур. |
| 3. | 2D-фигуры используются для показа на технических чертежах вида сверху, сбоку, снизу и спереди | 3D-фигуры используются для рисования изометрических и ортогональных фигур. |
| 4. | Гравюры, ранголис нарисованы на двухмерных фигурах, которые делают дизайн более красивым, так как он нарисован с помощью цветов. | Ранголис и гравюры трудно рисовать в трехмерных фигурах, так как они могут быть не такими идеальными, как в двухмерных фигурах. |
| 5. | Когда мы измеряем, чем 2 D формы имеет длину и ширину. | В 3-х мерной форме он также имеет длину, ширину и высоту. |
| 6. | Когда мы рисуем любой план структуры в 2D-форме, он дает обзор и объясняет все детали. | Рисуя изометрический вид (3D), он дает фактический вид конструкции. |
| 7. | Эти 2D формы широко используются для рисования простых изображений или эскизов простого объекта. | Трехмерная форма используется для определения архитектурного вида объекта. |
| 8. | Размеры можно легко объяснить. | Только внешние размеры могут быть объяснены. |
| 9. | В 2D фигурах все используемые края хорошо видны. | В 3D-фигурах некоторые ребра скрыты, и иногда нам приходится скрывать некоторые ребра, чтобы получить 3D-фигуру. |
| 10. | 2D-фигуры очень просто нарисовать, так как не нужно много думать, глядя на них. Он находит лучший способ нарисовать это легко. | Некоторые сложные формы в трехмерной структуре выглядят очень сложно, и пользователю трудно рисовать. Сначала он должен подумать, с чего начать, иначе структура может принять странную форму. |
Вывод:
Рассматривая разницу между 2D и 3D формами, мы должны знать их особенности и их использование. Из вышеизложенного делается вывод, что 2D является инициатором рисунка или фигур, где ученик должен сначала изучить это, а затем он должен сделать следующий шаг. Двухмерный рисунок состоит из нескольких правильных форм, которые помогают нам улучшить свои навыки рисования, а также повышают нашу точность.
Наконец, можно сделать вывод, что обе эти формы обладают уникальными качествами, что и для конкретных рисунков, которые мы должны выбрать. Таким образом, изучение всех сложных функций из 2D и 3D делает студента идеальным кандидатом на рисование.
Рекомендуемые статьи
Это было руководство к разнице между 2D и 3D формами. Здесь мы также обсудим ключевые различия 2D и 3D фигур с помощью инфографики и сравнительной таблицы. Вы также можете взглянуть на следующие статьи, чтобы узнать больше —
- AUTOCAD vs CATIA — главные отличия
- Photoshop vs InDesign
- QuarkXPress против InDesign
- 2D After Effects Animation
- Cinema 4D против Maya — какая из них лучше?
- Photoshop против Illustrator | Отличия от инфографики
Что такое трехмерные фигуры?
Что такое трехмерные фигуры? В геометрии трехмерная форма может быть определена как твердая фигура или объект или форма, имеющая три измерения — длину, ширину и высоту. В отличие от двумерных фигур трехмерные фигуры имеют толщину или глубину.
В отличие от двумерных фигур трехмерные фигуры имеют толщину или глубину.
Учитесь с полной программой обучения математике K-5
Атрибутами трехмерной фигуры являются грани, ребра и вершины.Три измерения составляют края трехмерной геометрической формы.
Куб, прямоугольная призма, сфера, конус и цилиндр — основные трехмерные формы, которые мы видим вокруг себя.
Мы можем видеть кубик в кубике Рубика и кубике, прямоугольную призму в книге и коробке, сферу в глобусе и шаре, рожок в морковке и рожке мороженого и цилиндр в ведерке и бочка, вокруг нас.
Вот список трехмерных или трехмерных фигур с их названиями, изображениями и атрибутами.
| Имя 3D-формы : | Изображение трехмерной формы : | Атрибуты : |
| Куб | Граней — 6 Ребер — 12 Вершин — 8 | |
| Прямоугольная призма или параллелепипед | Граней — 6 Ребер — 12 Вершин — 8 | |
| Сфера | Изогнутая грань — 1 Ребра — 0 Вершины — 0 | |
| Конус | Плоская грань — 1 Изогнутая грань — 1 Ребра — 1 Вершины — 1 | |
| Цилиндр | Плоская грань — 2 Изогнутая грань — 1 Ребра — 2 Вершины — 0 |
Интересные факты
|
Давайте петь!
3D-формы толстые, а не плоские.
Найди шишку в праздничной шапке!
Ты видишь сферу в баскетбольном мяче,
И прямоугольный параллелепипед в таком высоком здании!
Вы видите куб в кости, которую вы бросаете,
И цилиндр в блестящем флагштоке!
Давай сделаем это!
Вместо того чтобы показывать детям и детсадовцам видеоролики о трехмерных фигурах, попросите их понаблюдать и найти вокруг себя предметы, в которых они могут найти трехмерные фигуры.
Вы также можете попросить их идентифицировать и отсортировать трехмерную форму и ее атрибуты.
Связанный математический словарь
трехмерных фигур | SkillsYouNeed
На этой странице рассматриваются свойства трехмерных или «твердых» форм.
Двумерная фигура имеет длину и ширину. Трехмерная твердая форма также имеет глубину. Трехмерные формы по своей природе имеют внутреннее и внешнее, разделенные поверхностью.Все физические предметы, к которым можно прикоснуться, трехмерны.
Трехмерные формы по своей природе имеют внутреннее и внешнее, разделенные поверхностью.Все физические предметы, к которым можно прикоснуться, трехмерны.
На этой странице рассматриваются как прямолинейные тела, называемые многогранниками, которые основаны на многоугольниках, так и тела с кривыми, такие как шары, цилиндры и конусы.
Многогранники
Многогранники (или многогранники) представляют собой твердые фигуры с прямыми сторонами. Многогранники основаны на многоугольниках, двумерных плоских формах с прямыми линиями.
Подробнее о работе с полигонами см. на нашей странице Свойства полигонов.
Многогранники определяются как имеющие:
- Прямые ребра .
- Плоские стороны называются гранями .
- Углов, называемых вершинами .
Многогранники также часто определяются количеством ребер, граней и вершин, которые они имеют, а также тем, имеют ли их грани одинаковую форму и размер.:max_bytes(150000):strip_icc()/GettyImages-530022001-58acb3d83df78c345b9e0da1.jpg) Как и многоугольники, многогранники могут быть правильными (на основе правильных многоугольников) или неправильными (на основе неправильных многоугольников).Многогранники также могут быть вогнутыми или выпуклыми.
Как и многоугольники, многогранники могут быть правильными (на основе правильных многоугольников) или неправильными (на основе неправильных многоугольников).Многогранники также могут быть вогнутыми или выпуклыми.
Одним из самых простых и знакомых многогранников является куб. Куб — это правильный многогранник, имеющий шесть квадратных граней, 12 ребер и восемь вершин.
Правильные многогранники (Платоновые тела)
Пять правильных многогранников представляют собой особый класс многогранников, все грани которых идентичны, причем каждая грань является правильным многоугольником. Платоновых тел:
- Тетраэдр с четырьмя равносторонними треугольными гранями.
- Куб с шестью квадратными гранями.
- Октаэдр с восемью равносторонними треугольными гранями.
- Додекаэдр с двенадцатью пятиугольными гранями.
- Икосаэдр с двадцатью равносторонними треугольными гранями.

См. рисунок выше для иллюстрации каждого из этих правильных многогранников.
Что такое призма?
Призма — это любой многогранник, имеющий два совпадающих конца и плоские стороны .Если вы разрежете призму в любом месте по ее длине, параллельно ее концу, ее поперечное сечение будет таким же — вы получите две призмы. Стороны призмы параллелограмма — четырехгранные фигуры с двумя парами сторон одинаковой длины.
Антипризмы аналогичны обычным призмам тем, что их концы совпадают. Однако стороны антипризмы состоят из треугольников, а не из параллелограммов. Антипризмы могут стать очень сложными.
Что такое пирамида?
Пирамида — это многогранник с многоугольниками в основании , который соединяется с вершиной (верхняя точка) с прямыми сторонами.
Хотя мы склонны думать о пирамидах с квадратным основанием, вроде тех, что строили древние египтяне, на самом деле они могут иметь основание в виде любого многоугольника, правильного или неправильного. Кроме того, пирамида может иметь вершину прямо в центре своего основания, Прямоугольная пирамида , или может иметь вершину вне центра, когда это Наклонная пирамида .
Кроме того, пирамида может иметь вершину прямо в центре своего основания, Прямоугольная пирамида , или может иметь вершину вне центра, когда это Наклонная пирамида .
Более сложные многогранники
Существует еще много видов многогранников: симметричные и несимметричные, вогнутые и выпуклые.
Архимедовы тела, например , состоят как минимум из двух различных правильных многоугольников.
Усеченный куб (как показано на рисунке) представляет собой архимедово тело с 14 гранями. Шесть граней представляют собой правильные восьмиугольники, а остальные восемь — правильные (равносторонние) треугольники. Фигура имеет 36 ребер и 24 вершины (угла).
Трехмерные формы с кривыми
Твердые фигуры с изогнутыми или круглыми краями не являются многогранниками.Многогранники могут иметь только прямые стороны. Также см. нашу страницу о двумерных изогнутых формах.
Многие объекты вокруг вас будут иметь по крайней мере несколько кривых.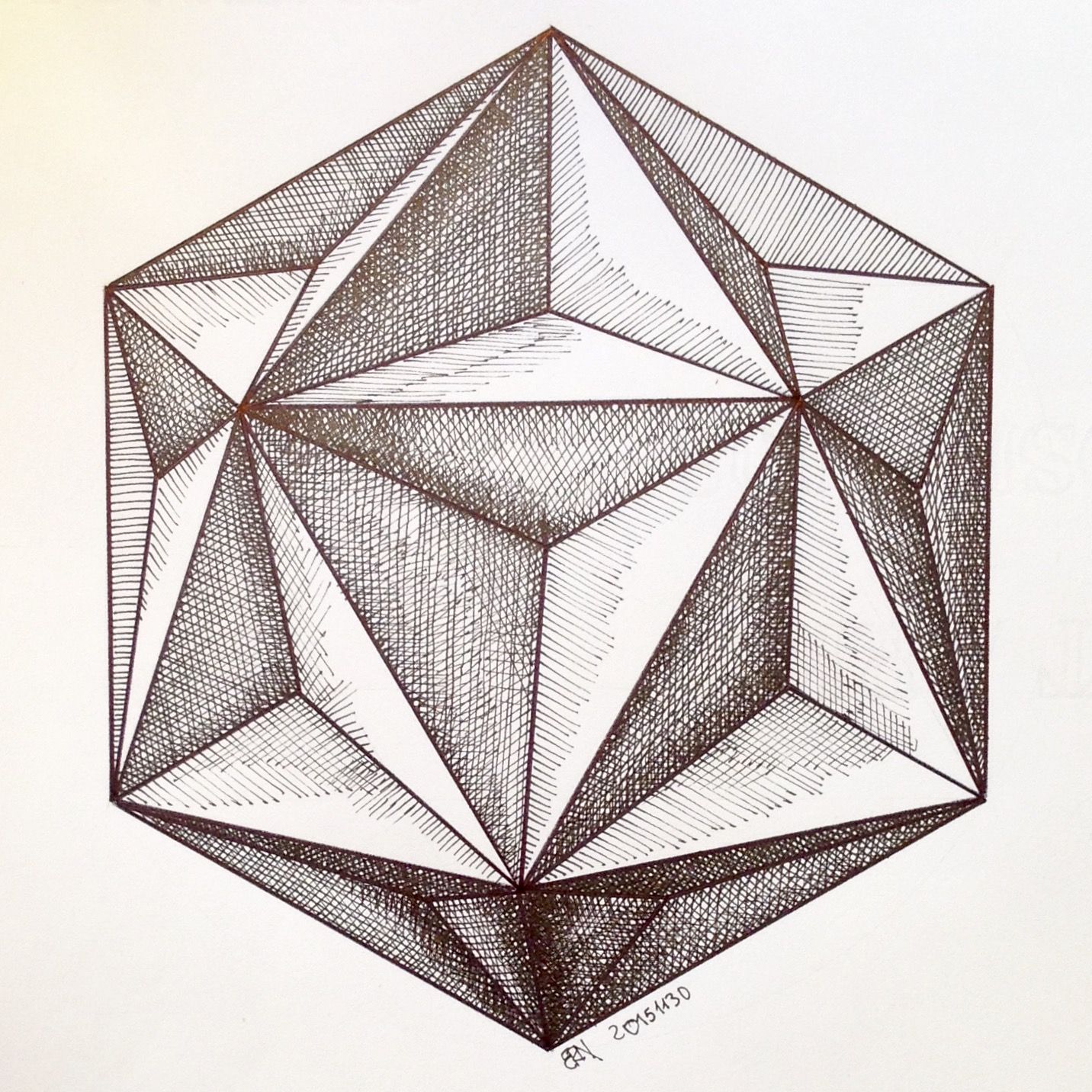 В геометрии наиболее распространенными искривленными телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
В геометрии наиболее распространенными искривленными телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
| Общие трехмерные формы с кривыми: | |
|---|---|
| Цилиндр | Конус |
| Цилиндр имеет одинаковое поперечное сечение от одного конца до другого.Цилиндры имеют два одинаковых конца либо круга, либо овала. Несмотря на то, что они похожи, цилиндры не являются призмами, поскольку призма имеет (по определению) параллелограмм с плоскими сторонами. | Конус имеет круглое или овальное основание и вершину (или вершину). Сторона конуса плавно сужается к вершине. Конус похож на пирамиду, но отличается тем, что конус имеет одну изогнутую сторону и круглое основание. |
| Сфера | Тор |
Сфера, имеющая форму шара или шара, представляет собой полностью круглый объект. Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. | Правильный кольцевой тор, имеющий форму кольца, шины или бублика, образован вращением меньшего круга вокруг большего круга. Существуют и более сложные формы торов. |
Площадь поверхности
На нашей странице, посвященной расчету площади, объясняется, как вычислить площадь двухмерных фигур, и вам необходимо понимать эти основы, чтобы вычислять площадь поверхности трехмерных фигур.
Для трехмерных фигур мы говорим о площади поверхности , чтобы избежать путаницы.
Вы можете использовать свои знания о площади двухмерных фигур для вычисления площади поверхности трехмерной фигуры, поскольку каждая грань или сторона фактически является двумерной фигурой.
Таким образом, вы вычисляете площадь каждой грани, а затем складываете их вместе.
Как и в случае с плоскими формами, площадь поверхности твердого тела выражается в квадратных единицах: см 2 , дюймы 2 , м 2 и так далее.![]() Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Примеры расчета площади поверхности
Куб
Площадь поверхности куба равна площади одной грани (длина х ширина), умноженной на 6, поскольку все шесть граней одинаковы.
Поскольку грань куба представляет собой квадрат, вам нужно выполнить только одно измерение — длина и ширина квадрата по определению одинаковы.
Следовательно, одна грань этого куба равна 10 × 10 см = 100 см 2 .Умножаем на 6 количество граней куба, и получаем, что площадь поверхности этого куба равна 600см 2 .
Прочие правильные многогранники
Точно так же площадь поверхности других правильных многогранников (платоновых тел) можно вычислить, найдя площадь одной стороны и затем умножив результат на общее количество сторон — см. диаграмму основных многогранников выше.
Если площадь одного пятиугольника, составляющего додекаэдр, равна 22см 2 , то умножьте это на общее количество сторон (12), чтобы получить ответ 264см 2 .
Пирамида
Для расчета площади поверхности стандартной пирамиды с четырьмя равными треугольными сторонами и квадратным основанием:
Сначала определите площадь основания (квадрата) длина × ширина.
Далее определите площадь одной стороны (треугольника). Измерьте ширину вдоль основания, а затем высоту треугольника (также известную как наклонная длина) от центральной точки основания до вершины.
Есть два способа вычислить площадь поверхности четырех треугольников:
Разделите ответ на 2, чтобы получить площадь поверхности одного треугольника, а затем умножьте на 4, чтобы получить площадь поверхности всех четырех сторон, или
Умножьте свой ответ на 2.
Наконец, сложите площадь основания и сторон вместе, чтобы найти общую площадь поверхности пирамиды.
Чтобы вычислить площади поверхности других типов пирамид, сложите площадь основания (известную как площадь основания) и площадь сторон (боковая площадь).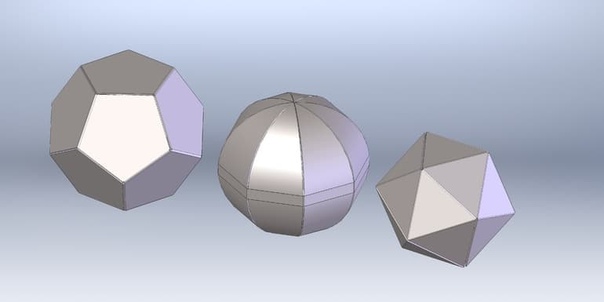 Возможно, вам придется измерить стороны по отдельности.
Возможно, вам придется измерить стороны по отдельности.
Диаграммы цепей
Геометрическая сеть — это двухмерный «шаблон» для трехмерного объекта. Сети могут быть полезны при расчете площади поверхности трехмерного объекта.На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды, если пирамида «развернута», у вас остается сеть.
Подробнее о схемах цепей см. на нашей странице 3D-фигуры и сети .
Призма
Для расчета площади поверхности призмы :
Призмы имеют два одинаковых конца и плоские стороны в виде параллелограмма.
Вычислите площадь одного конца и умножьте на 2.
Для правильной призмы (у которой все стороны одинаковы) вычислите площадь одной из сторон и умножьте на общее количество сторон.
Для призм неправильной формы (с разными сторонами) рассчитайте площадь каждой стороны.
Сложите два ответа вместе (концы + стороны), чтобы найти общую площадь поверхности призмы.
Цилиндр
Пример:
Радиус = 5 см
Высота = 10 см
Чтобы вычислить площадь поверхности цилиндра , полезно подумать о составных частях формы. Представьте себе банку сладкой кукурузы — у нее есть верх и низ, оба из которых представляют собой круги.Если вы отрежете сторону по длине и сгладите ее, у вас получится прямоугольник. Следовательно, вам нужно найти площадь двух кругов и прямоугольника.
Сначала определите площадь одного из кругов.
Площадь круга равна π (пи) × радиус 2 .
При радиусе 5 см площадь одного из кругов равна 3,14 × 5 2 = 78,5 см 2 .
Умножьте ответ на 2, так как кругов два 157см 2
Площадь стороны цилиндра равна периметру окружности × высоте цилиндра.
Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4
Измерьте высоту цилиндра. В данном примере высота равна 10 см. Площадь стороны 31,4 × 10 = 314см 2 .
Общая площадь поверхности может быть найдена путем сложения площади кругов и стороны вместе:
157 + 314 = 471см 2
Пример:
Радиус = 5 см
Длина наклона = 10 см
Конус
При расчете площади поверхности конуса необходимо использовать длину «наклона», а также радиус основания.
Однако вычислить его относительно просто:
Площадь круга в основании конуса составляет π (пи) × радиус 2 .
В этом примере расчет равен 3,14 × 5 2 = 3,14 × 25 = 78,5 см 2
Площадь стороны, наклонного сечения, можно найти по этой формуле:
π (пи) × радиус × длина наклона.
В нашем примере вычисление 3,14 × 5 × 10 = 157см 2 .
Наконец, добавьте площадь основания к площади боковой поверхности, чтобы получить общую площадь поверхности конуса.
78,5 + 157 = 235,5 см 2
Теннисный мяч:
Диаметр = 2,6 дюйма
Сфера
площадь поверхности сферы является относительно простым расширением формулы для площади круга.
4 × π × радиус 2 .
Для сферы часто проще измерить диаметр — расстояние поперек сферы.Затем вы можете найти радиус, который составляет половину диаметра.
Диаметр стандартного теннисного мяча составляет 2,6 дюйма. Таким образом, радиус составляет 1,3 дюйма. Для формулы нам нужен радиус в квадрате. 1,3 × 1,3 = 1,69
Площадь поверхности теннисного мяча равна:
4 × 3,14 × 1,69 = 21,2264 дюйма 2 .
Пример:
R (большой радиус) = 20 см
r (малый радиус) = 4 см
Тор
Чтобы вычислить площадь поверхности тора , вам нужно найти два значения радиуса.
Большой или большой радиус (R) измеряется от середины отверстия до середины кольца.
Малый или малый радиус (r) измеряется от середины кольца до внешнего края.
На диаграмме показаны два вида примера тора и способы измерения его радиусов (или радиусов).
Расчет площади поверхности состоит из двух частей (по одной для каждого радиуса). Расчет одинаков для каждой части.
Расчет одинаков для каждой части.
Формула: площадь поверхности = (2πR)(2πr)
Чтобы вычислить площадь поверхности примера тора.
(2 × π × R) = (2 × 3,14 × 20) = 125,6
(2 × π × r) = (2 × 3,14 × 4) = 25,12
Перемножьте два ответа вместе, чтобы найти общую площадь поверхности тора в примере.
125,6 × 25,12 = 3155,072 см 2 .
Дополнительное чтение из навыков, которые вам нужны
Понимание геометрии
Часть руководства по необходимым навыкам счета
В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства фигур, линий и тел.Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
Заполнение твердого тела: Том
При работе с трехмерными фигурами вам также может понадобиться знать, сколько объем они имеют.
Другими словами, если бы вы наполнили их водой или воздухом, сколько наполнения вам потребуется?
Это описано на нашей странице Расчет объема .
3-D фигурки в детском саду | Детский сад миссис Альбанезе, класс
Последние несколько недель мы изучали трехмерные фигуры.
Мы подготовили несколько различных провокаций, чтобы учащиеся поразмышляли над двухмерными (плоскими) и трехмерными (толстыми) формами посредством практических занятий (скоро будет фото!) . Мы концентрируемся в основном на 6 трехмерных фигурах (куб, конус, цилиндр, сфера, прямоугольная призма, пирамида), но у нас всегда есть другие фигуры в наших занятиях для изучения учащимися.Есть несколько математических ресурсов, которые являются моими абсолютными фаворитами! Если вы еще не читали их, то вам стоит подумать об этом (я читал и перечитывал их много раз!).
Кое-кто писал мне по электронной почте, спрашивая, где я купил различные 3D-фигурки, которые использую.
Мне также нравятся эти большие 3D-фигуры из пенопласта.Они от Scholastic Canada — если у вас есть бонусные купоны, я бы посоветовал использовать их для покупки нескольких таких наборов (вам не хватит!)
Мне также нравится читать эту книгу ученикам и предлагать им подумать о трехмерных фигурах в нашем классе.
Это отличная книга, объясняющая концепцию трехмерных фигур, которые могут катиться, скользить или делать и то, и другое!
Мы проверяем теории детей, используя пандусы и пенопластовые тела.
Мы также вместе начинаем составлять якорную диаграмму и учимся описывать каждую фигуру.
Эта песня Harry Kindergarten запоминающаяся и определенно любимая в нашем классе! Студенты просили об этом снова и снова!
ytimg.com/vi/2cg-Uc556-Q/0.jpg» frameborder=»0″ src=»https://www.youtube.com/embed/2cg-Uc556-Q?feature=player_embedded»/>
Как только дети освоятся с распознаванием трехмерных фигурок в мире, мы отправляем родителям письмо домой с просьбой прислать предметы из дома (лучше всего использовать вторсырье!), чтобы ученики могли их разобрать. Мы положили их все в нашу сенсорную корзину, а ученики рассортировали их на полках позади.
Мы поем эту песню во время обучения всей группы, чтобы повторить названия фигур.
Я раздаю 6 трехмерных фигур, о которых мы изучаем (куб, сфера, прямоугольная призма, пирамида, конус, цилиндр) некоторым ученикам. Если они держат фигуру, о которой я пою, они должны встать.
Им это нравится!
Помимо этих веселых песенок, мы читаем книгу по известному стихотворению о трехмерных фигурах.
Я превратил это стихотворение в большую книгу для учителя и прочитал ее со студентами.
Затем учащиеся могли сделать свои собственные книги меньшего размера на основе предсказуемых предложений. …»___ похож на ___.»
…»___ похож на ___.»
Я сделал эту книгу для учителя (она показана ниже в цвете) как книжку-раскладушку, что означает, что дается несколько подсказок, и ученики должны угадать фигуру, спрятанную под клапаном.
Ученикам так понравилась эта книга-загадка, что мы предложили им придумать свои собственные загадки «Подними клапан»!
В небольших группах я люблю играть в игру «Что в моей сумке?» Я использую маленькие пластиковые формы и кладу целую кучу в сумку.Вы можете играть по-разному:
* Попросите учащегося залезть в сумку. Перед тем, как вытащить трехмерную фигуру, он должен описать ее и записать свое предположение на рабочем листе, показанном ниже (у меня есть различные рабочие листы в зависимости от уровня, на котором находятся ученики. Проще всего поместить их в защитную пленку, чтобы мы могли просто стереть их). очистить и начать заново!)
* Та же идея, что и выше, но вы играете с другом, и этот человек угадывает, что это за трехмерная фигура.
У нас были студенты, которые использовали эти карточки для идентификации фигур, и они могли легко исправить себя, так как на обратной стороне была звезда.
Примечание: После печати я понял, что вместо вигвама была изображена палатка, и с тех пор это было исправлено.*
За одним из небольших провокационных столов в классе мы задали вопрос: «Можете ли вы построить башню из трехмерных фигур?» Я также включил небольшие клипы с 3D-фигурами, чтобы учащиеся могли документировать свои творения.
Вот очередную провокацию устроили:
«Сможешь построить?»
Учащиеся выбирают карточку и, используя маленькие трехмерные фигурки, пытаются ее собрать! Они должны выяснить, смогут ли они построить его или нет.
Это сделало инструмент отличной оценки !
Учащиеся могли бы объяснить , почему или , почему не , используя такой язык, как:
«Башня не устоит, если сфера окажется внизу, потому что она заставляет все с нее скатываться».
«Прямоугольная призма лучше всего подходит для начала башни, потому что она может складываться в обе стороны!» РС.
«Конус хорош наверху. Это как настоящий замок. У них есть вершины!» О.С.
«Этот не сработает — он начинался с конуса внизу, и вы не можете ничего положить сверху, потому что у него есть острие, и ничего не остается на острие». Г.А.
Мы добавили их в нашу карманную таблицу и предложили учащимся построить простые предложения со словами, используя трехмерные фигуры и примеры.
Мои ученики любят играть в игры — они никогда не отказываются от возможности присоединиться к небольшой группе, если я представил им забавную игру! Поэтому я создал «Захват 6» — игру, похожую на известную игру «Захват 4», но для победы вам нужно закрыть 6 ячеек рядом друг с другом на игровом поле (образуя прямоугольник).Им понравилась эта игра!
Вот еще одна игра, в которую мы играли — на этот раз всей компанией. ..
..
Возможно, вы уже видели это раньше — оно называется «У меня… у кого есть…»
Учащиеся говорят: «У меня есть…» и называют цвет и трехмерную фигуру, которую они видят на своей карточке, и говорят: «У кого есть…» и называют нижний значок (например, фиолетовый конус). Ученик, у которого есть эта фигура (например, фиолетовый конус), становится следующим. Игра продолжается до тех пор, пока не вернется к тому, кто начал.
(Нажмите на любую из картинок, чтобы перейти туда.)
загрузка..
Изучение трехмерных фигур ~ Маменькин уголок мира
Один из самых эффективных способов научить детей трехмерным фигурам — дать им практические возможности построить фигуры, как в упражнении зефирные фигуры . При работе с трехмерными фигурами детям может быть сложно визуализировать фигуры, просто глядя на рисунок на бумаге.Наблюдение за примерами из реальной жизни и, что еще лучше, создание самих фигур помогает им понять, как несколько двухмерных форм объединяются для создания трехмерных фигур.
Дети могут изучать множество трехмерных фигур, в том числе куб, треугольные и прямоугольные призмы и пирамиду на основе треугольника. Построение фигур знакомит детей с несколькими важными понятиями геометрии. Во-первых, детям легко определить стороны каждой фигуры.Например, куб состоит из шести квадратов, а прямоугольная призма состоит из двух квадратов и четырех прямоугольников.
Сборка трехмерных фигур также облегчает детям определение краев каждой фигуры. Ребенок может взять свою пирамиду с квадратным основанием и коснуться каждого края, получив в общей сложности восемь.
Еще одна важная концепция обучения при изучении трехмерных фигур — это количество углов или «вершин» у каждой фигуры. Как и ребра, ребенок может держать свою трехмерную фигуру и касаться каждой вершины.Например, куб имеет восемь вершин.
Изучая трехмерные фигуры, дети могут исследовать дополнительные свойства каждого твердого тела. Познакомить детей с понятиями скольжения, штабелирования и перекатывания. Такие фигуры, как кубы и призмы, могут скользить по поверхности и складываться друг на друга. Когда вы говорите с ребенком о том, почему определенные трехмерные фигуры могут скользить или складываться, а другие нет, это должно вызвать обсуждение о плоских гранях и кривых.
Такие фигуры, как кубы и призмы, могут скользить по поверхности и складываться друг на друга. Когда вы говорите с ребенком о том, почему определенные трехмерные фигуры могут скользить или складываться, а другие нет, это должно вызвать обсуждение о плоских гранях и кривых.
Чтобы обсудить катание, предложите ребенку попробовать свернуть некоторые из сделанных им фигур, например, куб или призму.Это поможет ему обнаружить, что эти фигуры не могут катиться из-за их плоских граней. Наоборот, такие фигуры, как сферы и конусы, могут катиться из-за своей изогнутой поверхности.
Наличие моделей каждой трехмерной фигуры может помочь детям сравнить их с формами в окружающей среде. Используя свои модели в качестве эталона, дети могут отправиться на «охоту» за 3D-фигурами дома, на улице или в других условиях. Попросите их найти повседневные предметы, сделанные из трехмерных фигурок.Например, банка из-под еды и чашка — это цилиндры, а коробка из-под обуви и коробка из-под хлопьев — прямоугольные призмы. Дети могут записывать свои выводы, рисуя объекты и обозначая, на какие трехмерные фигуры они похожи. Или, для детей младшего возраста, они могут просто сортировать найденные объекты, классифицируя их по каждой из своих 3D-моделей.
Дети могут записывать свои выводы, рисуя объекты и обозначая, на какие трехмерные фигуры они похожи. Или, для детей младшего возраста, они могут просто сортировать найденные объекты, классифицируя их по каждой из своих 3D-моделей.
В качестве дополнительной задачи попробуйте предложить ребенку загадки, которые помогут ему рассмотреть атрибуты каждой трехмерной фигуры. Например, загадкой может быть: «У меня шесть лиц, и все они квадратные.Какая я трехмерная фигура?» Или «У меня нет плоских лиц, и я не могу складываться или скользить. Какая я трехмерная фигура?»
Следующим шагом в их обучении будет предложить детям исследовать сетку каждой фигуры, двухмерный узор, который можно сложить, чтобы создать трехмерную форму. Изучение сетей помогает детям лучше понять, как 2D-формы создают плоские стороны 3D-фигур.
Создание трехмерных фигур, изучение их характеристик и использование их для сравнения повседневных предметов поможет детям понять трехмерные формы в увлекательной и конкретной форме.
2D- и 3D-фигуры – объяснение, разница между 2D- и 3D-формами, примеры решения
Геометрия – это изучение форм. Он широко подразделяется на два типа: плоская геометрия, называемая 2d-формами, и объемная геометрия, называемая 3d-формами. Нарисуем блокнот на листе бумаги. То, что мы наблюдаем, является простой картинкой, нарисованной на бумаге. Он не занимает никакого пространства, называемого двумерными фигурами, но если мы держим на этом листе бумаги настоящую записную книжку, он занимает некоторое пространство, и такие фигуры называются трехмерными фигурами или трехмерными формами.
Плоскостная геометрия или двухмерная геометрия имеет дело с плоскими фигурами, которые можно нарисовать на листе бумаги, такими как линии, кривые, многоугольники, четырехугольники и т. д., в то время как объемная геометрия или трехмерная геометрия имеет дело с объемными формами или формы. Примерами трехмерных фигур являются сферы, цилиндры, конусы и т. д.
[Изображение будет загружено в ближайшее время]
Что такое 2D-фигуры?
В геометрии форма или фигура, которая имеет два измерения, а именно длину и ширину, называется двумерной формой. Другими словами, плоский объект, имеющий только длину и ширину, является двумерной формой. Прямые или изогнутые линии составляют стороны этой формы. Также эти фигуры могут иметь любое количество сторон.
Другими словами, плоский объект, имеющий только длину и ширину, является двумерной формой. Прямые или изогнутые линии составляют стороны этой формы. Также эти фигуры могут иметь любое количество сторон.
Нет фиксированных свойств 2D-формы. Поскольку каждая форма имеет разное количество сторон, свойства каждой формы различаются. Но каждая 2D-форма плоская и замкнутая.
Многоугольником называется двумерная замкнутая фигура, ограниченная тремя или более тремя прямыми линиями.Треугольники, квадрат, прямоугольник, пятиугольник, шестиугольник — вот некоторые примеры многоугольников.
Например, треугольники и квадраты являются многоугольниками.
Примеры 2D-фигур:
[Изображение будет загружено в ближайшее время]
Что такое 3D-фигуры?
Фигуры, занимающие пространство, называются трехмерными фигурами. 3D-формы также могут быть определены как твердые формы, имеющие три измерения: длину, ширину и высоту. Примером сферы, представляющей собой трехмерную фигуру, является футбольный мяч, а нарисованный на листе бумаги круг — двухмерная фигура.Точно так же нас окружает множество трехмерных фигур, таких как стол, стул, блокнот, ручка и т. д. Вот несколько примеров трехмерных форм и свойств трехмерных фигур.
Примером сферы, представляющей собой трехмерную фигуру, является футбольный мяч, а нарисованный на листе бумаги круг — двухмерная фигура.Точно так же нас окружает множество трехмерных фигур, таких как стол, стул, блокнот, ручка и т. д. Вот несколько примеров трехмерных форм и свойств трехмерных фигур.
[Изображение будет загружено в ближайшее время]
Некоторые атрибуты трехмерных фигур:
Лица: Двумерные фигуры трехмерных фигур называются гранями трехмерных фигур.
Края: сегмент линии, образованный двумя гранями, называется краем трехмерных фигур.
Вершины: угловая точка, где встречаются края трехмерных фигур, называется вершиной.
Давайте рассмотрим трехмерную фигуру, куб. На рисунке ниже представлены грани, ребра и вершины куба.
[Изображение скоро будет загружено]
Вот разница между 2D и 3D формами, которая сделает концепцию более понятной.
Разница между 2D и 3D формы
| 1 2d формы | 1 3D формы | |||
| 1 Basic | только 2 измерения это длина и ширина. | Три измерения: длина, ширина и высота. | ||
| 1 Формы | квадрат, круг, треугольник, прямоугольник, шестиугольник и т. Д. | Куб, сфера, конус, Cuboid и др. | ||
| 1 включает в себя | длина Ширина | длина, ширина и высота | ||
| 1 Простые для создания | 1 Довольно комплекс | |||
| 1 кромки | полностью видны на чертежах. | Не видно или скрыто из-за наложения. Однако, если взять пример куба, то невозможно отобразить все его ребра под одним углом 1: Найдите объем и площадь поверхности прямоугольного параллелепипеда с l = 10 см, b = 8 см и h = 6 см. Решение: у нас есть объем Cuboid = V = LXBXH = 10 x 8 x 6 = 480CM2 площадь поверхности = 2 (LB + LH + BH) = 2 (10×8 + 10×6 + 8×6) =2(80 + 60 + 48) =376см2 Пример 2: Длина прямоугольного поля 15м, ширина 6м.Найти область и периметр поля Раствор : Учитывая, что длина = 15 м ширина = 6 м у нас есть, область формулы A = длина х ширина = 15 х 60009 = 90 м2 и Формула периметра P = 2 (длина + ширина) = 2 x (15 + 6) = 2 x 21 = 42 м. Quiz Time Найдите площадь прямоугольного треугольника, основание которого равно 12 см, а гипотенуза 13 см.
Сторона квадрата, чей площадь 600 см составляет 90 см30 см 40 см Интересные факты Названия трехмерных фигур, трехмерные фигуры и их названияИмена 3D-фигур, 3D-фигуры и их названия Имена 3D-фигур В этом уроке мы подробно рассмотрим тему «Имена трехмерных фигур». Объект, ограниченный двумя параллельными поверхностями, которые вертикально пересекают ось объекта, нижнее и верхнее основания которого состоят из равных друг другу кругов. Другими словами, это геометрическая трехмерная форма, образованная кругом, совершающим неплоское поступательное движение. Если направление движения перпендикулярно окружности, то получившийся валик называется перпендикулярным валиком, если нет – косым валиком.
Куб — это трехмерная геометрическая трехмерная фигура, состоящая из шести квадратов, площади которых равны друг другу с прямыми углами.
В геометрии кубоид — это выпуклый многогранник, ограниченный шестигранной четверной гранью, многогранник которой такой же, как у куба.
Конус — это геометрическая трехмерная фигура, созданная отрезками линий, которые соединяют каждую точку круга на плоскости с точкой вне плоскости в математике. Конус, полученный при повороте прямоугольного треугольника вокруг правого ребра, называется крутым конусом или вращающимся конусом.
Пирамида представляет собой n-гранный многогранник, посаженный на n-конечное многоугольное основание, соединяющее треугольные поверхности на одном холме.
При повседневном использовании сфера представляет собой геометрический объект с идеальной симметрией, это поверхность; лежит в трехмерном евклидовом пространстве.В повседневном использовании твердый объект называется сферой.
Полушарие или полушарие — это название, данное каждой из половин на востоке и западе, когда предполагается, что земля разделена экватором по экватору, с его продольными половинами на севере и юге.
Так как призмы называются по форме их оснований, призмы с треугольным основанием называются треугольными призмами.
Основаниями равносторонней треугольной призмы являются равносторонние треугольники.Его боковые поверхности состоят из трех одинаковых прямоугольников.
Основанием прямоугольной призмы является прямоугольный треугольник. Боковые поверхности состоят из трех прямоугольников.
Шестиугольная призма имеет много граней, стороны которых прямоугольные с двумя основаниями, одним внизу и одним вверху.Шестиугольная призма: имеет 12 сторон, 18 сторон и 8 граней. Элементы: высота основания длина ребра Шестиугольная призма, как и другие призмы, бывает двух видов.
Поверхность бублика в топологии и геометрии. Получается вращением окружности в трехмерном пространстве вокруг линии, лежащей в той же плоскости и не касающейся окружности. Поверхность бублика или надутого пузыря, используемого для плавания, математически является бубликом.Форма тора также сформулирована как математический образец. Форма яблока и тора известна как тор. Форма тора присутствует на многих устройствах, содержащих жизнь. Существует модель тора на вращении Земли, планет, Солнечной системы, самолета, летающей тарелки и атома. Некоторые ученые считают, что форма Вселенной также соответствует модели тора. Энергия в паттерне Тора течет к одному концу, вращаясь вокруг центра, и выходит с другого конца.Это хаотическая система, которая приспосабливается и уравновешивается. Другими словами, энергия в центре действует как черная дыра на одном конце и белая дыра на другом.
Пятиугольная призма — это тип призмы с пятиугольными основаниями. Они состоят из двух пиров и параллельных баз. Он бывает двух видов: косой и крутой.Боковые грани представляют собой параллельные ребра в косых призмах, боковые грани прямоугольные или квадратные в прямых призмах.
Эллипсоид является поверхностью второго порядка, и его пересечение с любой плоскостью является эллипсом. Он имеет симметричную форму относительно трех осей, перпендикулярных друг другу, называемых главными осями и центром этих осей.
3D фигурки для детского сада: Руки на центры и печатные материалыПоследнее обновление: 07.14.17 — Все новые клип-арт и шрифты — 105 страниц Добавлено — 6-дневные планы урок с учебными планами программы детского сада Онтарио, 2016 г. ДОБАВЛЕНО ________________________________________________________ Эта трехмерная фигурка, протестированная в классе, включает: стр.5-8: Музей 3D-фигур: Объяснение упражнения, образец исходной буквы и знаки/ярлыки для musuem (этикетки также можно использовать в качестве карточек со словами для вашей математической стены) стр. стр. 23-54: мини-плакаты с 3D-фигурами в 2 вариантах шрифта, с QR-кодами и без них: конус, куб, цилиндр, призма, сфера, пирамида, прямоугольник Призма, треугольная призма стр. 55-64: Создание трехмерных рисунков: Карточки для построения шаблонов AB, ABB, AAB и ABC стр.65-72: Упражнение по рисованию, маркировке и сортировке трехмерных фигур стр. 73-77: Карточки с трехмерными фигурками Зефир и зубочистка стр. 78-107: Моя книга трехмерных фигурок: включены 4 версии, только для чтения, прослеживание трехмерной графики фигурное слово, обведите все предложение и заполните пропуск. стр.108-115: Какой может быть фигура? Мини-книга: попросите учащихся определить трехмерные фигуры из реальной жизни, нарисовать и написать о них в этом буклете стр. 116-125: 3D-фигуры в нашей жизни (для начинающих читателей) стр. 125: Таблица примеров из реальной жизни трехмерных фигурок р. p.129-147: 3D Figure Tracing Book p.148-151: Race to the Finish Line (Настольная игра) p.152-161: 3D Figure BINGO p .162-191: Маты и карточки для сортировки 3D-фигурок + Редактируемое письмо родителей музея 3D-фигурок (Powerpoint, 2 варианта) Пожалуйста, загрузите предварительную версию, чтобы получить бесплатную поэму 3D-фигурки! Вы можете увидеть это устройство в действии в моем блоге по адресу http://apinchofkinder.blogspot.ca/2014/11/teaching-3d-figures-in-fdk.HTML Этот продукт включен в эти пакеты: — детские сады математические центры: год длинного пакета — детский сад математические единицы: геометрия Пожалуйста, не покупайте это, если у вас есть любой из ЭТИ ПАКЕТЫ! ———————————————————————————————————————— Сопутствующие товары: • 2D-фигуры для детского сада • Симметрия для детского сада • Сортировка для детского сада —————————————————————— ———————————————————— Ищете больше? Уделите немного времени ИССЛЕДОВАНИЮ! ♦ Пакеты ♦ Математика ♦ Грамотность ♦ ЛУЧШИЕ ПРОДАЖИ Редактируемый учебный портфель . |





 «Остроконечный» 3D doodle позволяет создавать фигуры с острыми углами и идеально подходит, например, для рисования звезд. «Плавный» 3D doodle позволяет рисовать плавные линии, замечательно подходящие для изображения облаков.
«Остроконечный» 3D doodle позволяет создавать фигуры с острыми углами и идеально подходит, например, для рисования звезд. «Плавный» 3D doodle позволяет рисовать плавные линии, замечательно подходящие для изображения облаков. Двумерный текст выравнивается по холсту и закрепляется на нем, тогда как трехмерный можно перемещать и вращать в разных направлениях.
Двумерный текст выравнивается по холсту и закрепляется на нем, тогда как трехмерный можно перемещать и вращать в разных направлениях.

 В трехмерных формах эта детализация невозможна.
В трехмерных формах эта детализация невозможна.
 Например, у квадрата видны все грани.
Например, у квадрата видны все грани.
 Имена трехмерных фигур — это проблема, с которой мы можем столкнуться в повседневной жизни. Имена трехмерных фигур общие:
Имена трехмерных фигур — это проблема, с которой мы можем столкнуться в повседневной жизни. Имена трехмерных фигур общие: Его также называют гладким шестигранным и является одним из 5 платоновых тел.Важнейшей особенностью куба является то, что все грани квадратные. Его объем находится путем умножения 3 равных.
Его также называют гладким шестигранным и является одним из 5 платоновых тел.Важнейшей особенностью куба является то, что все грани квадратные. Его объем находится путем умножения 3 равных.



 9-22: Карманная схема 3D-фигурок Поэма: Полное стихотворение в цвете и ч/б, а также 2 версии карманной поэмы
9-22: Карманная схема 3D-фигурок Поэма: Полное стихотворение в цвете и ч/б, а также 2 версии карманной поэмы 127-128: 3D Figure Crown
127-128: 3D Figure Crown